Error, Equilibrium, and Equilibration in Austrian Price Theory

Volume 17, No. 2 (Summer 2014)

ABSTRACT: Theorists of the Austrian school have long maintained that every realized price is market-clearing, in sharp contrast to the adherents of the neoclassical mainstream, who view realized prices as constituting a state of disequilibrium with a mismatch between demand and supply. The heart of these theoretical differences lies in the equilibrium constructs used by the members of the two schools of thought in their analysis of price formation. This paper seeks to clarify and develop1 the conceptual foundations underlying the Austrian position, especially the concept of the plain state of rest, which represents a state of market equilibrium with error. It also provides a brief sketch of the role that realized prices play in the process of error correction and entrepreneurial selection that forms a key part of the market process as described by Ludwig von Mises.

KEYWORDS: Austrian school, equilibrium, entrepreneurship, Walrasian, disequilibrium, neoclassicism

JEL CLASSIFICATION: B53, B25, B21, D51

I. INTRODUCTION

Theorists working in the tradition of the Austrian school have consistently maintained that every realized price establishes a momentary equilibrium between demand and supply and exhausts all the potential gains from trade. This maxim was enunciated by Carl Menger, the founder of the school, who in his pathbreaking Principles of Economics noted that “the prices of goods are symptoms of an economic equilibrium in the distribution of possessions between the economies of individuals” (Menger, 2007 [1871], p. 192), a conclusion echoed by his immediate follower Eugen von Böhm-Bawerk, who described such a “momentary equilibrium” not as “a metaphorical analogy” but “as living reality (Böhm-Bawerk, 1959, pp. 229, 231).” The leading “Mengerians” in the early twentieth century were equally emphatic. Frank Fetter led the way, arguing that “any price, no matter how temporary and unstable, is one that for the moment brings into equilibrium the quantities bought and sold, produced and wanted at that price (Fetter, 1910, p. 133),” while Herbert Davenport was just as categorical, stating that “every price level is, for its particular time, the point at which the supply and demand arrive at an equilibrium (Davenport, 1929 [1913], p. 42).”

In the post-World War II era, this proposition received further emphasis in the works of Ludwig von Mises and William Hutt. Mises, for instance, observed that “at any instant (on the market place) all those transactions take place which the parties are ready to enter into at the realizable price,” with only “those potential sellers and buyers who consider the market price too low or too high” abstaining from buying or selling (Mises, 1998 [1949], p. 245). Similarly, Hutt, that venerable foe of the Keynesians, argued that whereas “‘potential supplies’ of and ‘potential demands’ for things (at different values or prices) may be represented in supply schedules and demand schedules…actual supplies and actual demands are identical magnitudes with identical values or prices at the point of intersection of those schedules (Hutt, 2007 [1974], p. 15).”

The most elaborate and conclusive defense of the proposition that every realized price is market-clearing, however, was provided by Arthur Marget in his magnum opus The Theory of Prices (Marget, 1966, p. 231–263). While emphasizing that “the goal of any Theory of Prices, like that of any part of economics which undertakes to explain economic reality, is to explain why realized prices are what they are (Marget, 1966, p. 222, emphasis in the original),” Marget went on to argue that “the only type of “equilibrium” which is necessarily involved in the establishment of any “realized” price is an “equilibrium” between (in the sense of an equality of) the quantity demanded and the quantity supplied at a given price (Marget, 1966, p. 232, emphasis in the original).”

These claims of economists working in the Mengerian tradition stand in sharp contrast to the views of their neoclassical colleagues, who, for ultimate inspiration, look not to Menger but to two other giants of the economics scene of the late nineteenth century—Léon Walras and Alfred Marshall. J.R. Hicks, whose work is probably the best embodiment of this neoclassical Walrasian-Marshallian synthesis, believed that exchanges would most likely be made at disequilibrium prices; prices at which demand and supply will not be equated. In other words, Hicks believed that realized prices are not market-clearing in nature and that the construct of equilibrium is unrealistic and inapplicable to the economic phenomena of the real world.

Thus, commenting on Walras’ analysis of price formation in a pure exchange scenario, i.e., with given stocks of goods, Hicks states that “if there is no actual exchange until the equilibrium prices are reached by bidding, then Walras’ argument is beyond reproach on the score of logical consistency, although it may be called unrealistic (Hicks, 1934, p. 342, emphasis added).”2 Similarly, in his famous note on price formation in his treatise Value and Capital, Hicks first notes that “since, in general, traders cannot be expected to know just what total supplies are available on the market, nor what total demands will be forthcoming at particular prices, any price which is fixed initially can only be a guess,” and then concludes that “it is not probable that demand and supply will actually be found to be equated at such a guessed price.” It is to describe such realized disequilibrium prices that Hicks coined the phrase “false prices,” while defining exchanges made at such prices as “false trades (Hicks, 1946 [1939], pp. 127–128, emphasis added).”

In order to understand these differences between the Mengerian economists and their neoclassical colleagues, it is vital to note that in a pure exchange scenario (the only scenario that this paper considers), the former make use of two types of equilibrium constructs in order to gain an understanding of price formation.3 They employ, first, the inherently unrealistic construct of an equilibrium or a state of rest without any error; a state in which all market participants are engaging in action that is optimal. In addition, they also utilize the eminently realistic construct of an equilibrium with error, i.e., a state of rest that does not involve optimal action on the part of market participants. Indeed, as this paper seeks to illustrate, the latter concept is key to understanding the claim that all realized prices are market-clearing in nature. Moreover, it is also the key to clarifying the differences between the Austrian and neoclassical understanding of realized prices, since the latter employ only one equilibrium construct (in the pure exchange scenario), namely, the unrealistic one of an error-free equilibrium.

As mentioned above, the analysis in this paper is confined to the realm of a pure exchange economy, one in which the stocks of the goods being exchanged are assumed to be fixed and in which the complications introduced by the production of goods are completely ignored. The model utilized is an adaptation of the canonical Austrian pure exchange model, that of the horse market, first introduced by Menger (Menger, 2007 [1871], pp. 197–225) in his treatment of price formation and then made famous by Böhm-Bawerk (Böhm-Bawerk, 1959, pp. 215–235).

Section II of the paper lays out the basic structure of our model as well as the assumptions underlying the analysis that follows. Section III focuses on the error-free equilibrium construct. This section introduces and develops the crucial difference between the original valuations with which the market participants enter the market and the momentary valuations that prevail at the moment when the exchanges are completed. A grasp of these two concepts and the differences between them is crucial to understanding the construct of an equilibrium with error, which is developed in detail in section IV. Section V of the paper provides a brief adumbration of the process of error correction that operates on the market, all the while paying close attention to the crucial role that the error-filled, realized prices play in this process, while section VI summarizes the arguments developed during the course of the paper, thereby providing a conclusion.

II. THE HORSE MARKET

Consider a small horse market in an isolated village. Potential buyers arrive on the market ready to offer sums of money in exchange for horses; whereas the potential sellers possess horses they are willing to part with for the right sums of money. The maximum buying prices, i.e., the maximum amounts of money that buyers are willing to part with for each additional horse are depicted in Table 1 below:

Table 1.

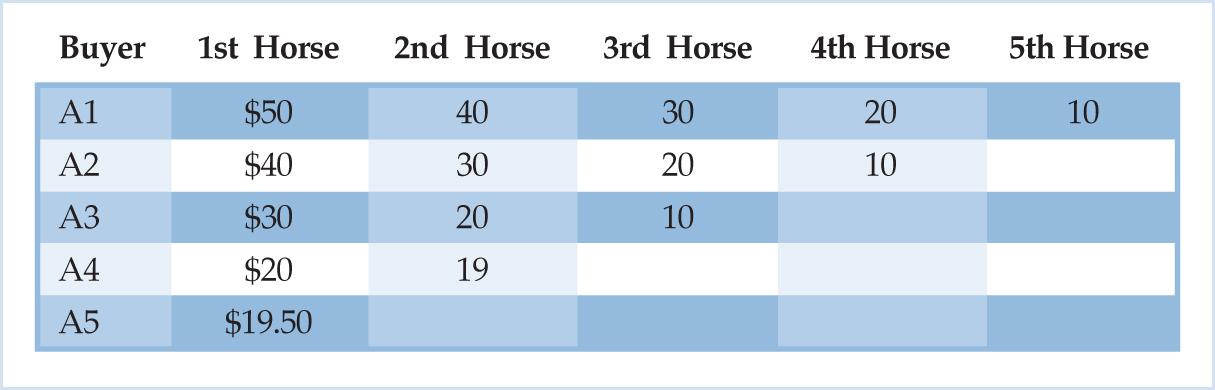
This list of maximum buying prices represents a snapshot of the value scales of each potential buyer when he enters the market. Each buyer places a valuation on an additional horse, a result of a comparison of the respective marginal utilities of the horse and a sum of money. Consider buyer A1, who is willing to part with a maximum of $50 for his first horse and ten dollars less for each subsequent horse. How did he arrive at these precise sums of money that he is willing to pay for each additional horse? He did so by comparing the marginal utility of the additional horse and the marginal utility of the sum of money, a comparison made in his “given situation” when he enters the market, i.e., with his given endowment of money and horses and his prevailing scale of ends. His willingness to part with the $50 for the horse shows that he ranks his first horse above that amount of money since the former’s marginal utility exceeds that of the latter.

There are, as can be seen, altogether five potential buyers of horses in our market. Given that the law of diminishing marginal utility applies to both horses as well as money, each buyer is willing to pay a smaller amount for each additional horse that he considers purchasing. Each additional horse will be used to serve an end ranked lower than that which the previous horse satisfied, and each additional sum of money has to be withdrawn from the service of an end or a complex of ends that ranks higher on the buyer’s value scale.

Standing athwart our five buyers are two potential sellers with five horses apiece. Like our buyers, each seller also places a valuation on each horse that he possesses; a certain minimum monetary sum that he is willing to accept in exchange for giving up the horse. These minimum selling prices of the two sellers are depicted in Table 2 below:

Table 2.

It is clear from the table that both the potential sellers place a minimum price of $0 on all the horses in their possession, an indication that they are willing to sell each of them for any positive sum of money. These minimum selling prices are a reflection of the fact that both B1 and B2 receive no marginal utility from any of the horses in their possession. Stated differently, there is no end for either of them that is dependent on the possession of a horse and that would remain unsatisfied if they were to lose a horse. Just like the buyers, B1 and B2 also form these rankings of their horses against sums of money in the given situation that they find themselves in when they enter the market, i.e., given their endowments of money and horses and their prevailing scale of ends.

The five buyers and two sellers are assumed to enter our imaginary market at the beginning of a market day. Their prevailing value scales (depicted in Tables 1 and 2) reflect their rankings of units of horses relative to sums of money as they enter the market. In the following analysis, it will be assumed that these initial valuations, which can also be termed original valuations, stay unchanged through the course of the given market day, i.e., as long as the market remains open for business. These original valuations, along with the stock of horses available for sale, can thus be said to constitute the underlying data of our market scenario. Moreover, it is also assumed that no market for horses exists in the foreseeable future, depriving sellers of the option of carrying over and selling any unsold horses on future market days. As a result, they must sell all the horses that they wish to by the end of the given market day.

The original valuations of our potential market participants throw up a host of opportunities for both buyers and sellers to make themselves better off by engaging in exchange. Indeed, the maximum buying prices of all the potential buyers for each additional horse are above the minimum selling prices placed by sellers B1 and B2 on the horses in their possession. In other words, there are a number of instances in which a buyer ranks a horse above a certain sum of money and a seller ranks those two things in reverse, thereby resulting in a reverse valuation that can be exploited via an exchange. By swapping the sum of money for the horse, the buyer obtains a good that he values more and thus ranks higher for one that he values less, thereby making himself better off. And the seller does likewise; he gives up a good he values less for a good he ranks higher, and thus achieves an improvement in his well-being.

III. THE FINAL STATE OF REST

Let us assume that B1 and B2 are endowed with perfect knowledge of the prevailing market conditions. Blessed with the ability to read the value scales of all the other market participants, each seller gains a window into the minds of his competitor and all the potential buyers. He learns that, just like him, the other seller also enters the market with five horses and a minimum supply price of $0 for each of them, enabling him to reconstruct the “original supply schedule” derived from the original valuations of the sellers. He knows, therefore, that all ten horses possessed by the sellers will be forthcoming for sale at any positive price.

Similarly, each seller is also in a position to know the maximum sum of money that each buyer is willing to part with for each additional horse, allowing him to form a correct estimation of the underlying “original demand schedule” that emerges from the original valuations of the potential buyers. In other words, he knows how many horses the buyers are willing to buy at any given price.

Upon reconstructing these original demand and supply schedules, each seller learns that our imaginary market clears at the price of $20, with the quantity of horses that buyers are willing to purchase at this price equaling the amount that is forthcoming on the part of the sellers, i.e., the entire stock of ten horses in their possession. At any other price, however, there is a mismatch between the quantities demanded and supplied. For instance, at a price below $20, the amount that buyers are willing to buy exceeds the amount that sellers are willing to part with, whereas the opposite scenario prevails at a price above $20, with the quantity supplied at such a price outstripping the quantity demanded.

Each seller undertakes this appraisement of the underlying market conditions in order to find the price that will maximize the flow of monetary revenue from the stock of horses in his possession. For while he would prefer to sell his horses for any positive sum of money, his preference for more money as compared to less makes him aim at selling them for the highest possible price. Thus, he endeavors to obtain an understanding of the given market situation in which he operates and the data underlying it so as to allocate each of his horses to satisfy the ends that he values the most, namely, that of obtaining the highest possible sums of money in exchange.

Now, based on his knowledge of the prevailing original demand and supply schedules, B1 concludes that it would be a mistake to sell any of his horses at a price below $20. For at any price below $20, the quantity of horses that buyers are willing to purchase exceeds the quantity of horses forthcoming for sale and it would pay for him to raise his asking price since he could sell his entire stock of horses at a higher price. In other words, the sale of any horses below the price of $20 would be at odds with his goal of maximizing the monetary revenue earned.

Similarly, B1 also realizes that any attempt to price a horse above $20 would ultimately prove to be counterproductive. For if he were to try and outfox B2 by pricing his stock of horses at a price higher than $20, B2 could out-compete him by pricing his horses a little lower, and as a result B1 would earn less revenue than he would have at the price of $20.

To understand why this is the case, let us examine the underlying data of our market in more detail. From the information presented in Table 1, it is clear that at the price of $20 the available stock of horses can satisfy the demands of all those buyers who value a horse at $20 or more. Buyer A1, for instance, would buy four horses at this price since he ranks his first four horses above the sum of $20, while the other buyers would do likewise; they would all purchase horses as long as an additional horse is ranked above $20.

Now, assume that B1 prices the horses in his stall at $30, indicating to the buyers that this price is non-negotiable. B2 could respond by pricing his horses slightly lower, say, at $29. This would induce the buyers who trickle into the marketplace to avoid B1’s stall and instead make all their purchases at B2’s stall. B2 would thus have no trouble in selling his entire stock of five horses at this price, with his horses being purchased by buyers who rank an additional horse above the sum of $29.

These purchases made at the price of $29, however, would reduce the remaining demand for horses at the initial market-clearing price of $20. To begin with, some of the buyers who would have happily bought a horse at the price of $20 have now made their purchases at the price of $29 instead. A1, for instance, purchases three horses at this price, although he would have been just as willing to purchase them at $20. This is the first factor making for a reduced demand at $20.

There is, moreover, a second factor at work. Some of the demand for horses on the part of buyers who would have purchased horses at $20 has now been effectively destroyed due to their decision to purchase horses at $29. Thus, A1 has a demand for four horses at the price of $20, but buys only three horses at the price of $29 before exiting the market, thereby destroying his demand for that fourth horse at $20. Similarly, A4, who leaves the market empty-handed when the price is $29, would have purchased one horse if the price had been $20. His exit from the market, however, implies that his demand for that first horse at $20 has now disappeared.

Thus, if B1 were to now revise his asking price down to $20, he would find himself unable to sell his stock of five horses at this price. For as a result of the two factors described above, the quantity of horses demanded at the price of $20 is no longer five horses but a lower quantity, which implies that B1 would have to lower his asking price below the figure of $20 in order to sell his stock of five horses. Thus, B1’s attempt to earn more revenue by pricing his horses above what he knows to be the final price necessarily ends in frustration. His revenues are now lower than what they would have been if he had priced his horses at $20 from the beginning. Meanwhile, the coffers of his competitor are now fuller, since he was able to sell his horses at the higher price of $29.4

Thus, B1 and B2 both decide to price the horses in their stalls at $20 apiece while buyers, in turn, trickle into the marketplace through the day and decide whether or not to make purchases at this price. As is evident from table one above, at the price of $20 buyer A1 is willing to buy four horses, whereas buyers A2, A3 and A4 are willing to buy three, two and one horse respectively. Buyer A5, meanwhile, leaves the market empty-handed since his first horse is ranked below the prevailing price. Thus, by the end of the market day all ten horses have been sold, with the sellers successfully getting rid of their entire stock of horses.

It is vital to note that the valuations of the sellers at the moment when these exchanges are made differ from the original valuations with which they entered our imaginary market. For when they initially entered the market, the sellers were willing to part with their horses for any sum of money. However, their appraisements of the original demand and supply schedules led them to revise these original valuations, giving rise to “momentary valuations” and a “momentary supply schedule” that prevails at the moment when the sellers decide to exchange their horses for sums of money offered by the buyers5 .Far from being willing to sell all of their horses at any positive price, B1 and B2 now choose to price their horses at $20, thereby indicating that they prefer to withhold their horses rather than sell them at a lower price.

All realized prices, in fact, are the result of the momentary valuations of the buyers and sellers that prevail at the moment when the exchanges are made.6 In the analysis above, we assumed that only sellers have perfect knowledge and appraise the underlying market conditions, while buyers make their purchases without engaging in any appraisement. Thus, the momentary value scales of the buyers at the moment when they make their exchanges do not differ from their original valuations, thereby implying that the momentary and original demand curves are identical.

One can, however, assume that buyers also have perfect knowledge and that they too try to gain an understanding of the prevailing market conditions. Blessed with this ability to reconstruct the original demand and supply curves, each buyer, given that he would like to buy an additional horse at the cheapest price possible, re-adjusts his maximum buying prices to ensure that he does not pay more than he has to for a horse. Each buyer knows that at prices below $20 the quantity of horses supplied exceeds the quantity demanded. He thus concludes that it would be a mistake to pay anything more than $20 for a horse and proceeds to re-adjust his maximum buying prices that were above this price downwards, giving rise to the momentary valuation that underlie the momentary demand curve (which would no longer be identical to the original demand curve).7 , 8

The realized price of $20 has several interesting proerties that are worth analyzing in more detail. First, the sale of all ten horses at this “final price” brings our market to a “final state of rest.”9

I have, however, chosen to stick with Mises’s terminology for two reasons. First, and most importantly, the conclusions derived during the course of the following analysis on the relationship between the momentary and original valuations and therefore on the relationship between the error-free equilibrium (the final state of rest) and the equilibrium with error (the plain state of rest) are equally valid in both a pure exchange scenario as well as in a scenario with production. Second, in light of this, I believe that the benefits derived from the avoidance of a multiplication of terms exceed the costs of any potential misinterpretation of the results derived.

Given his prevailing value scale,10 no market participant has any further incentive to act at this price, for he has successfully exploited all the available opportunities to give up a good that he values less in exchange for a good that he values more. Thus, every buyer who ranks an additional horse above $20 has made his purchases, whereas every seller who values $20 more than a horse in his possession has parted with it, while the solitary buyer who finds no horse preferable to $20 has chosen to stay out of the market altogether.

Second, this final price is market-clearing in two ways. To begin with, it lies at the intersection of the original demand and supply schedules. Reading off Tables 1 and 2 above, the quantity of horses that buyers would be willing to buy at the price of $20 equals the number of horses that sellers would wish to put up for sale. However, the final price can also be said to lie at the intersection of the momentary demand and supply schedules that prevail at the moment when the buyers and sellers engage in the acts of exchange. The reason that it lies at the intersection of both sets of demand and supply schedules is the assumption of perfect knowledge and the resulting correct appraisement of the original valuations by both the sellers.11 The momentary supply schedule, in other words, is a faithful reflection of the underlying data.12

Third, at the final price the available stock of horses finds its way into the hands of the most capable possessors, i.e., those individuals that place the highest monetary valuations on an additional horse. If we were to line up the maximum buying prices as shown in table one in descending order we would place A1’s valuation of $50 for his first horse right at the top, A1 and A2’s willingness to pay $40 second, etc. Now, if we were to distribute the ten horses amongst the ten highest bidders, we would end up with precisely the distribution that emerges when exchanges take place at the final price of $20. In both cases the horses finally end up in the hands of buyers A1 through A4, with A1 leading the way with four horses followed by A2, A3 and A4 with three, two and one horse respectively.

This brings us to the fourth and arguably most important characteristic of the final price: that it is error-free. A final price only emerges when market participants make choices on the basis of a correct appraisement of the prevailing original valuations. In other words, a final price is the result of momentary demand and supply schedules that are free of error and are a faithful reflection of the underlying original demand and supply curves.13

When neoclassical economists refer to an equilibrium price, it is the final price that they have in mind. However, given its error-free nature, such a price will be seldom realized in the real world.14 For while in our example we have assumed perfect knowledge on the part of the sellers, this unrealistic assumption never holds true in reality. Human beings, by nature, are denied the gift of omniscience and are thus liable to make errors in their estimations of the given market conditions, giving rise to prices that differ from the final price.

Thus, neoclassicals are consistent in maintaining that equilibrium prices are unrealistic and are different from the actual prices realized in real world markets. But what if final prices are not the only kind of equilibrium prices? What if realized prices that are not error-free are also equilibrium, market-clearing prices? In the following section, we turn to answering this question.

IV. THE PLAIN STATE OF REST

Let us drop the assumption of perfect knowledge on the part of the sellers. Each seller must now appraise the original valuations of the other market participants without the gift of omniscience. Both sellers will, nevertheless, try to form an understanding of the underlying data in an attempt to sell their horses for the highest possible price.

Given, however, that this understanding of the prevailing scenario is formed without perfect knowledge, both sellers could arrive at erroneous conclusions regarding the underlying original demand and supply schedules. Thus, B1, for instance, might overestimate the maximum buying prices of the buyers and might, as a result, arrive at the erroneous conclusion that the final price is $30. We now assume that B2 makes an identical incorrect estimation of the underlying conditions and also comes to believe that the final price for this market is $30.

Based on these erroneous momentary valuations, the sellers proceed to price the stock of horses they have on hand. For reasons identical to those discussed in the previous section, both of them decide to sell their horses at a price of $30, the price that they incorrectly believe is the final price for this market. Thus the momentary valuations formed by B1 and B2 in a state of imperfect knowledge yield a fresh momentary supply curve, different from the one that was based on the correct momentary valuations formed in a state of perfect knowledge.

The buyers, as they trickle into the market, find the horses at the stalls of both sellers priced at $30 apiece. Given their original valuations (that, by assumption, coincide with their momentary valuations) they purchase horses as long as they rank an additional horse above the price asked. As is evident by studying Table 1 (reproduced below), six horses are bought at the price of $30, with buyer A1 purchasing three horses and buyers A2 and A3 going home with two and one horse respectively. Buyers A4 and A5, on the other hand, stay out of the market completely since neither of them values his first horse above the asking price of $30.

Table 1.

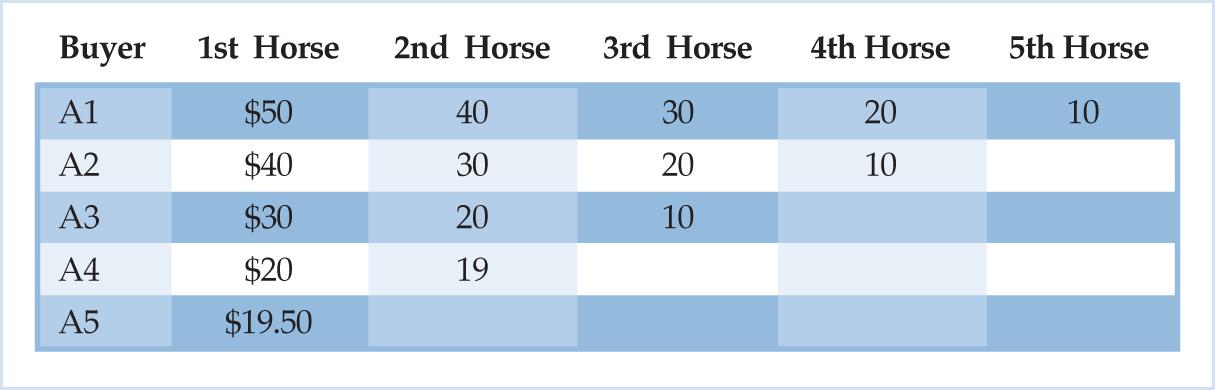
Remember that each seller enters the market at the beginning of the market day with a minimum selling price of $0 for every horse in his possession. Thus, carrying home unsold horses at the end of the market day would be a sub-optimal situation for him given that he derives no marginal utility from any of the horses in his possession. Instead, each seller would prefer to sell his entire stock of horses for any positive price. Nevertheless, despite the fact that sales are sluggish at the price of $30, the sellers leave their asking price unchanged. Both of them are supremely confident in their assessments of the ultimate facts of the market and believe that all their horses will find willing buyers by the end of the day.

The realized price of $30 has several interesting characteristics that are worth examining. First, just like the final price, this price too brings our horse market to a state of rest, or a state of non-action. Once the six horses are exchanged, all our market participants have successfully exploited all opportunities to acquire a good that they rank higher on their value scales in exchange for one that they rank lower and thus no buyer or seller has any incentive to act given his momentary valuations. Every buyer who ranks one or more additional horses above the price of $30 has bought them and every seller who values the $30 more than a horse in his possession has successfully sold it. Meanwhile, the buyers who do not participate in the exchange process do not value any horse above the asking price, whereas the unsold horses in the stalls of the sellers at the end of the market day reflect their preference to hold on to them rather than sell them for a price less than $30.15

Second, the realized price of $30 lies at the intersection of the momentary demand and supply curves. Given the value scales of the market participants that prevail at the moment the exchanges are made, this price clears the market, with every willing buyer successful in finding a willing seller. Now, it is true that these prevailing momentary valuations of the sellers contain error, since they are the result of an erroneous appraisement of the underlying original valuations. Indeed, at the end of the market day the sellers will go home disappointed. They will realize, in retrospect, that they have erred in their judgment of the underlying market conditions and will therefore tell themselves that they should not have continued to maintain an asking price of $30 when sales were slow but should have dropped their price so as to sell their entire stock of horses.

Nevertheless, at the moment when the buyers made their choices of how many horses to buy, the sellers were only willing to part with a horse if the buyer paid $30. Their momentary value scales ranked a horse in their possession above any price less than $30 and they preferred to hold on to them rather than part with them for any smaller sum of money. Thus, at the moment when the exchanges were made, the number of horses that the sellers were willing to sell or the quantity of horses supplied is only six, which is equal to the quantity demanded.16 This, however, is different from the quantity that they planned or that they wished to sell at the price of $30 when they formed their appraisement of market conditions.17

The market-clearing nature of the plain state of rest can also be understood if we keep the necessary conditions required to engage in exchange firmly in mind. As Menger pointed out in his Principles of Economics, three conditions are essential for any act of exchange to take place, namely:

(a) one economizing individual must have command of quantities of goods which have a smaller value to him than other quantities of goods at the disposal of another economizing individual who evaluates the goods in reverse fashion, (b) the two economizing individuals must have recognized this relationship, (c) they must have the power actually to perform the exchange of goods. (Menger, 2007 [1871], p. 180)

Once the potential buyers have left the market making the purchases that they wish to make at the price of $30, however, condition (a) is no longer satisfied and the necessary conditions for interpersonal exchanges to be made no longer exists. There are no buyers present who have command of sums of money with a desire to purchase a horse. Thus, there are no further reverse valuations to be exploited since none exist and there are no more willing buyers to take the remaining unsold horses off the hands of the sellers at their asking price. Nevertheless, as long as the necessary conditions for exchange are present, every willing buyer finds a willing seller and vice versa.

Now, while the price of $30 does lie at the intersection of the momentary demand and supply schedules, it does not lie at the intersection of the underlying original demand and supply schedules. As is evident from Tables 1 and 2, at the price of $30 the original valuations of the market participants do not generate a market-clearing outcome. Instead, at this price there is an excess of the quantity of horses supplied over the quantity demanded. But as has been stressed above, the valuations of the market participants (only the sellers in our example) at the moment when they enter into market transactions is different from the valuations with which they entered the market. And it is the erroneous nature of the prevailing momentary supply schedule that explains why the price of $30 does not lie at the intersection of the original demand and supply schedules.

Coming now to the third characteristic of the realized price of $30, it follows from the discussion above that the state of rest established by this price is a market equilibrium with error. It can thus be termed a “plain state of rest (Mises 1998 [1949], p. 246)” in order to distinguish it from the final state of rest, which represents an equilibrium that is free of all error on the part of the market participants. The choices of our market participants at the plain state of rest (PSR) price are, unlike those made at the final price, not optimal. The sellers do not achieve their goal of selling all their horses at any positive price and end up having to take four horses back home.

The erroneous nature of the plain state of rest also affects the distribution of the available stock of horses amongst its competing claimants. If we consider the original valuations of the market participants, it is evident that the horses do not end up in the possession of the most capable possessors. This is evident from the fact that four horses remain unsold in the hands of the sellers, who place a $0 valuation on them, while there are buyers who evaluate an additional horse at a higher sum. For instance, buyers A1 through A3 place a higher monetary valuation on an additional horse despite already possessing horses that they purchased at the price of $30, while A4 and A5 have a higher valuation of their first horses.

Nevertheless, when the momentary valuations of the market participants are considered, one can conclude that the stock of horses is in the hands of the most capable possessors once the six exchanges have been made. For in this case, all those individuals who place a valuation of $30 or higher on a horse possess one, whereas those who have a lower monetary valuation of a horse do not possess any. It is true that the sellers only value the horses in their possession at $30 due to an erroneous understanding of the given market conditions. But they nevertheless choose to hold on to them.18

Now the buyers would walk into the market to find the horses priced at a much lower $10 and would proceed to make their purchases. Given their prevailing value scales as they enter the market, each buyer will buy as long as he ranks an additional horse above $10. As a result, all ten horses fly off the shelves at this price. Assuming A1 is the first buyer to enter the market and A2 follows, the former purchases five and latter four horses. When A3 enters, he has just the solitary horse available for purchase. The sellers, confident in their assessment of the underlying market conditions, leave their prices unchanged despite the rapid pace of their sales. They continue to believe that $10 is the highest price at which they can sell all the horses in their possession and that there will be unsold stocks at any higher price.

Thus, given the prevailing value scales of the buyers and sellers, the price of $10 also exhausts all the potential gains from trade and clears the market, thereby establishing a plain state of rest. In other words, it lies at the intersection of the momentary demand and supply curves that prevail as long as the market remains open for business and the possibility of engaging in exchange exists. And this holds true despite the fact that the sellers erroneously underpriced their horses, resulting in buyers who go home disappointed. For A3, A4 and A5 would have all been willing to buy more horses at the price of $10, but are unable to do so since the shelves of the sellers are empty. However, once A3 purchases the last remaining horse, the necessary conditions for an interpersonal exchange are no longer present since condition (a) is no longer satisfied. The sellers no longer have command of any horses that they could potentially sell, and as a result, no reverse valuations exist even though A3, A4 and A5 would prefer to purchase more horses at the prevailing price. Stated differently, the absence of the necessary conditions for an exchange implies that our market comes to a close once the last horse is sold to A3. Thus, as long as the necessary conditions for an exchange are present and our market is open for business, every willing buyer finds a willing seller and the quantity of horses demanded equals the quantity supplied.

Thus, when Austrian or Mengerian economists claim that every realized price is market-clearing, they are referring to PSR prices and not final prices. Given that human beings do not possess perfect knowledge and thus are bound to make appraisements that are erroneous in nature, realized prices represent equilibrium with error. Final prices, as the neoclassicals emphasize, are unrealistic and unrealizable.

V. THE ERROR CORRECTION PROCESS

In the previous section, we showed that the prices realized during the course of exchange in real world markets are market-clearing, equilibrium prices that establish a plain state of rest. They result from the momentary valuations of buyers and sellers; valuations that contain error due to an incorrect appraisement of the ultimate facts underlying the given market scenario. Thus, although actual prices realized in clock time do establish a state of equilibrium, they nevertheless contain error and result in a less than optimal distribution of resources. In our example, the ten horses do not find their way into the hands of the most capable possessors. Instead, at the end of the market day, four of them remain in the hands of the sellers who value them at $0 despite the fact that there were potential buyers who were willing to pay a positive price in exchange for these horses while the market was in operation.

The question that now arises is whether there are any forces operating on the market that succeed in correcting these erroneous judgments made by market participants. In other words, are there any forces that work to establish a more optimal allocation of resources? And what role, if any, do the actual, real world PSR prices play in this process? This section seeks to provide an answer to these questions.

To begin with, let us drop the assumption that both sellers make an identical incorrect assessment of the underlying data. This, after all, is an assumption with little empirical justification. To the contrary, one would expect each individual to form a different understanding of the data. Moreover, some individuals would be better appraisers of market conditions than others. Indeed, it can be assumed that the inherent skill of sizing up the original valuations underlying any given market situation is not distributed uniformly across human beings.19

Thus, we now assume that B2 is the better appraiser of the two sellers. While B1 overestimates the maximum buying prices of the potential buyers and concludes that the final price is $30, B2 does better. Given his lack of omniscience he too makes an erroneous judgment of the underlying data and overestimates the final price; but his guess of $25 is less incorrect than that of his competitor.

Now, based on his assessment of the underlying market conditions, B1 proceeds to price his horses at the rate of $30. B2, meanwhile, responds by raising his price to a little below B1’s, say $29, thereby outcompeting him. The buyers who trickle into the market proceed to buy only from B2, shunning B1’s stall. B1, however, has supreme confidence in his judgment and believes that it is B2 who is making an error by pricing below what he believes is the final price. Thus, he makes no adjustments to his asking price.

For reasons identical to those we described in section II,20 the price that B1 will be able to obtain for his stock of horses once the purchases at $29 have been made from B2’s stall will be lower than the original final price of $20. The errors of B1 have hurt him, reducing his revenue, while benefitting his competitor who could take advantage of his errors, not because he was blessed with perfect knowledge of the underlying data, but because he was a better appraiser than B1. In the words of Wicksteed:

…if any dealer correctly surmises that his rivals are standing out for a higher price than the state of market justifies, he may raise his own price above it too, so long as he is careful to keep below that of his rivals, knowing that while he is getting more they will ultimately have to take less than what is now the true equilibrating price (Wicksteed, 1910, p. 225).

Similarly, if we assume that B1 had initially underestimated the final price and B2 had done likewise, but had come closer to guessing the correct final price, a similar conclusion would follow. B1, say, believes that the final price is $10, whereas B2 believes it is $15. Thus, B1 proceeds to price his stock at $10 and B2 places a price tag of $15 on his horses. All the buyers initially make a beeline for the former’s stall and ignore that of the latter. B1, noticing that all the buyers are making their purchases from him, raises his price to $14, just below that of B2’s, and proceeds to sell his entire stock of horses at that price. B2, meanwhile, holds firm and does not lower his price. He is confident in his judgment that the final price is $15.

Now, as we noted in section II, at the price of $20 the available stock of horses can satisfy all those buyers who value a unit of a horse above this asking price. It thus follows that if five horses are sold at a lower price of $14, some purchases are made at this price that would not have been made if the price had been set at $20. Buyer A1, for instance, would purchase five horses at this price, whereas he would have bought only four at the final price. Similarly, buyer A4 would now buy two horses instead of one. Thus, some of the five horses sold by B1 at this lower price serve purposes that would not have been served at the higher price of $20.

As a result, once B1 sells his stock of horses at the price of $14, his competitor is able to sell his five horses at a price that exceeds the underlying final price. In other words, B2 is able to sell his horses at a price that exceeds $20. Once more, the errors of B1 have benefitted his competitor, who is the superior appraiser.

Thus, on any market, as a general rule, the revenues of the better appraisers exceed those of the sellers less adept at judging the underlying data. And as can be seen from our analysis above, the PSR prices that are formed as a result of exchanges taking place at every moment on the market perform a key role in deciding this allocation of revenue. Stated differently, assuming that the costs of production for all the sellers are equal, the sellers that form a better appraisement of the final price and who therefore have momentary valuations that are relatively less erroneous earn a higher rate of profit. Indeed, depending on the prevailing cost of production, the poorer appraisers might not only earn a lower rate of profit but might also earn a loss.

These differential rates of profits and losses that emerge as a result of the different appraisements made by the sellers will lead to a re-allocation of the pool of capital available for investment. Thus, the better appraisers, by earning a higher rate of profit gain a greater share of this available pool, at the expense of the poorer appraisers, who earn lower rates of profit or fail to break even. In the words of Mises,

…one of the main functions of profits is to shift the control of capital to those who know how to employ it in the best possible way for the satisfaction of the public. The more profits a man earns, the greater his wealth consequently becomes, the more influential does he become in the conduct of business affairs. (Mises, 2008 [1951], p. 23)

Now, given that the underlying data of any market is characterized by ceaseless flux, the sellers are forced to be on their toes, constantly trying to form an understanding of the prevailing original valuations of the market participants. Each market day throws up a fresh set of original valuations and might involve changes in the stock of horses available for sale, thereby requiring fresh appraisements and new momentary valuations on the part of the sellers. It follows that those sellers who consistently misread the market conditions will be gradually forced to exit the market and will be replaced by those sellers who are blessed with superior abilities of appraisement.

Thus, the process of error correction on the market is essentially one of entrepreneurial selection.21 Given the lack of omniscience and the constantly changing data, errors are never completely eliminated except by sheer chance. Instead, the market ensures that the best appraisers are the ones given the responsibility of reading the underlying data and pricing the available stock of goods, thereby ensuring that the allocation of the same is as optimal as possible given the inherent frailties of men.

VI. CONCLUSION

Economic theorists working within the broad Mengerian tradition conceive of the actual market prices realized in clock time as being market-clearing in nature. These prices thrown up by the exchange process undertaken in real world markets are said to establish momentary equilibria, with an equality of the quantities demanded and supplied and an exhaustion of all potential gains from trade. This view contrast sharply with those of the economists comprising the neoclassical mainstream, who instead view realized prices as disequilibrium prices, with a prevailing inequality of supply and demand.

The heart of these differences lies in the equilibrium constructs used by the proponents of the two schools of thought in a pure exchange setting. The Austrian economists employ two different equilibrium constructs in their explanation of price formation, namely, an equilibrium with error and an another without error. The former, also termed the plain state of rest, is inherently realistic in nature, whereas the latter, termed the final state of rest, is not. The neoclassicals, however, employ only the latter construct in their theorizing.

The conceptual foundations of the Austrian view lie in the differentiation between original and momentary valuations. Whereas the former reflect the value scales of market participants when they enter the market at the beginning of the market day, the latter are those that prevail at the moment when exchanges are made during the course of the given day, and are the formed by the buyers and sellers after an appraisement of the underlying data of the market, i.e., the prevailing original valuations.

The final price that brings about the final state of rest clears the market given the original valuations. At this price all the market participants are making choices that are optimal given the valuations with which they entered the market. PSR prices, meanwhile, establish a state of rest that is a result of the momentary valuations that prevail at the moment when exchanges are made during the market day. Thus, while they lie at the intersection of the momentary demand and supply schedules; they do not, given the erroneous appraisements of the market participants, clear the market given the original valuations. In other words, while they are market-clearing from one point of view, they are not from another. Moreover, they establish equilibria that contain error, with the buyers and sellers making sub-optimal choices given the underlying market conditions.

These PSR prices play a key role in the process of error correction that is unceasingly at work on the marketplace. These moment-to-moment prices decide the winners and losers of the exchange process, with the better appraisers earning greater profits than those that are poorer at judging the underlying data, thereby shifting the available pool of capital into the hands of the former at the expense of the latter. As a result, the exchange process selects who is entrusted with the job of appraising the underlying data and pricing the goods available for sale, with those that prove themselves to be the best equipped to gauge the underlying market conditions by consistently outdoing their competitors being the ones given the responsibility of making these decisions.

1G.P. Manish (gmanish@troy.edu) is Assistant Professor of Economics at the Manuel Johnson Center for Political Economy, Troy University. is Assistant Professor of Economics at the Manuel Johnson Center for Political Economy, Troy University.
2For similar assessments of Walras’ equilibrium construct in a pure exchange setting see Schumpeter (1963 [1954], p. 1008-09), Patinkin (1956, appendix on Walras’ tatonnement), and Donzelli (2007). For an identical interpretation of Marshall’s treatment of equilibrium in a pure exchange economy (his ultra-short period equilibrium), see De Vroey (1999).
3For the various equilibrium constructs utilized by the Mengerian economists both in a pure exchange setting as well as in a scenario allowing for production and the associated changes in the stocks of goods available for sale, see Salerno (1993, 1994, 1999) and Klein (2010, pp. 125–150).
4Stated differently, the demand curve facing each individual seller is elastic above the price at which the entire stock of horses available can be sold. For a more elaborate discussion of this proposition, see Salerno (2003) and the sources cited therein.
5In the words of Phillip Wicksteed, “…whenever equilibrium does not exist, and the conditions for exchange are present, the persons conducting the exchanges attempt to form an intelligent estimate of the price which would produce equilibrium, and the result of that attempt fixes the actual terms on which all the exchanges in the open market are for the moment made (Wicksteed, 1910, p. 214).”
6As Davenport notes, “The actual price at any instant is fixed by the demand bids as they are and the supply offers as they are, and by nothing else—by the actual rather than the potential facts (Davenport, 1929 [1913], p. 43).” Davenport uses the term “actual facts” to refer to what I have termed momentary valuations while the “potential facts” that he refers to correspond to the underlying data or the original valuations.
7As described by Marget, “…it is of course perfectly possible that the demand and supply schedules of the bargainers may themselves change in the process of bargaining. In the case under discussion, this means (1) that the original demand schedules, for example, may change when some demanders discover that the price they would have been willing to pay is higher than they need to pay; or (2) that the original supply schedules may change when some suppliers discover that the price that they would have been willing to accept is less than that which they need accept (Marget, 1966, p. 232, fn. 25).”
8In the rest of the analysis below, we will continue to assume that only sellers appraise the underlying valuations of market participants and that buyers do not do so. This assumption, however, does not affect any of the conclusions derived in the paper.I have, however, chosen to stick with Mises’s terminology for two reasons. First, and most importantly, the conclusions derived during the course of the following analysis on the relationship between the momentary and original valuations and therefore on the relationship between the error-free equilibrium (the final state of rest) and the equilibrium with error (the plain state of rest) are equally valid in both a pure exchange scenario as well as in a scenario with production. Second, in light of this, I believe that the benefits derived from the avoidance of a multiplication of terms exceed the costs of any potential misinterpretation of the results derived.I have, however, chosen to stick with Mises’s terminology for two reasons. First, and most importantly, the conclusions derived during the course of the following analysis on the relationship between the momentary and original valuations and therefore on the relationship between the error-free equilibrium (the final state of rest) and the equilibrium with error (the plain state of rest) are equally valid in both a pure exchange scenario as well as in a scenario with production. Second, in light of this, I believe that the benefits derived from the avoidance of a multiplication of terms exceed the costs of any potential misinterpretation of the results derived.
9The terms “final state of rest” and “final price” were first used by Mises (Mises, 1998 [1949], p. 246) to denote the state of long run equilibrium where all the factors of production have been allocated to their highest valued ends and no firm earns a profit or loss and the prices that prevail in such a state respectively. Given that our analysis is conducted in a pure exchange scenario where the stocks of goods are assumed to be given and all problems associated with production and the allocation of the factors of production are assumed away, an argument can be made for the use of another term to describe the price that clears the market given the underlying data in such a scenario. Indeed, others have chosen to go down this route. Professor Salerno, for example, has used the term “Wicksteedian State of Rest” to describe such a price (Salerno, 1994, p. 99). Alternately, one could follow Frank Fetter and term such a price “the logical or theoretical price (Fetter, 1915, p. 66 and fn. 5 on p. 66).”
10Value scales that reflect the momentary valuations of both sellers and buyers, although given our assumptions the momentary and original valuations of the buyers coincide.
11Thus, as Wicksteed notes, “…if we could eliminate all error from speculative estimates and could reduce derivative preferences [momentary valuations] to exact correspondence with the primary preferences [original valuations] which they represent, and on which they are based, the actual price would always correspond with the ideal price [final price] (Wicksteed, 1910, p. 237).”
12For a graphical illustration of this proposition see Rothbard (2009 [1962]), pp. 132–134.
13Professor Kirzner provides an excellent analysis of the emergence as well as the salient properties of the final price given the assumption of perfect knowledge on the part of market participants in Kirzner (2011 [1963]), pp. 113–120)
14See the quotation of Hicks from Value and Capital in the introduction, where he makes the same argument.
15In the words of Mises, “…people keep on exchanging on the market until no further exchange is possible because no party expects any further improvement of its own conditions from a new act of exchange. The potential buyers consider the prices asked by the potential sellers unsatisfactory, and vice versa. No more transactions take place. A state of rest emerges. This state of rest, which we call the plain state of rest, is not merely an imaginary construct. It comes to pass again and again (Mises, 1998 [1949], p. 245).”
16Stated differently, at any realized price there can be no “discrepancy between demand price and supply price” for the quantity actually sold and bought. “For if the sale of a given amount of a commodity is effected at a given price, this must mean that the seller was willing to sell that amount at that price, and that the buyer was willing to buy that amount at that price” (Marget, 1966, pp. 242–243, emphasis in the original).
17“…the realized prices which may be sufficient to move successive parts of the stores from the market may not necessarily be the same as the price which would have removed the whole if, again in Marshall’s own words, a single price had been “fixed on at the beginning and adhered to throughout”(Marget, 1966, p. 233, emphasis in the original).
18A similar plain state of rest would also emerge if the sellers underestimate the final price instead of overestimating it. Thus, they might misread the original demand curve and conclude that the available stock of horses in the market will sell at a price as low as $10; an incorrect appraisal that gives rise to a new momentary supply curve.
19“The operation of the market reflects the fact that changes in the data are first perceived only by a few people and that different men draw different conclusions in appraising their effects. The more enterprising and brighter individuals take the lead, others follow later. The shrewder individuals appreciate conditions more correctly than the less intelligent and therefore succeed better in their actions. Economists must never disregard in their reasoning the fact that the innate and acquired inequality of men differentiates their adjustment to the conditions of their environment” (Mises, 1998 [1949], p. 325).
20See pp. 9–10 above.
21On the selective process inherent in the market process see Mises, (1998 [1949], p. 308–310).