As the Austrian School economists know full well, inflation distorts price signals unevenly. It may be tempting to try to filter out inflation from any given good or service to find its real price had the currency supply never been inflated in the first place, but this is impossible given the uneven effects. Inflationary effects on prices cannot truly be isolated and controlled for.
But what about money itself? Meaning, what about gold? Currency is always inflated on top of the existing money (currently gold) supply, so the price of gold is actually what is being falsely inflated. Therefore, controlling the price of money itself in order to find the real price (which could be seen as gold’s real purchasing power) sans inflation is much more plausible by numerical or statistical analysis.
From an analysis of gold priced in terms of 1959 USD, which in effect strips out the inflation effect on the gold/dollar exchange rate, there is a massive consolidating triangle pattern going back to 1980 that is now reaching its apex. From an analysis of this pattern, it seems that gold is about to break out to the upside in current dollar terms. Below we explain how we came to this conclusion.
Chart 1 is a plot of the USD M2 currency supply from 1959 to December 2023. The dashed curve (1) is an exponential fit to that data from 1959 to 2020. The data after the 2020 COVID Pandemic does not follow the exponential trend line due to the extreme credit creation via quantitative easing (QE4) in the COVID years. Therefore we have used a 5th order polynomial fit, dashed curve (2), to model the expansion of the M2 money supply. That is, we have had to treat these two periods, pre and post 2020, separately.
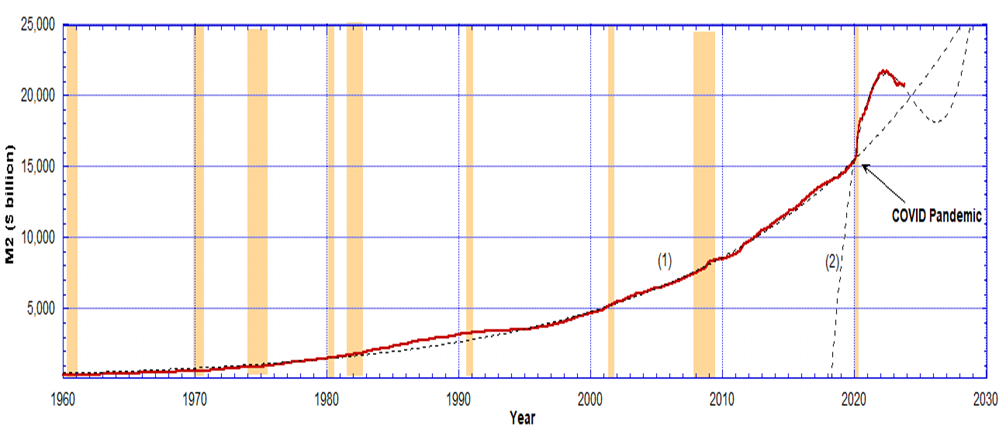
Chart 1: The red data are the M2 currency supply data for 1959–2023 from the Board of Governors of the Federal Reserve System,statistical release H.6 Money Stock Measures, via FRED. The dashed curve (1) is an exponential fit to the data between 1959 and 2020. The dashed curve (2) is a 5th order polynomial fit to the data after 2020 up to December 2023. After normalisation the M2 supply becomes essentially constant (not shown). Sepia strips indicate recessions.
From Chart 1, we used the exponential fit curve, the dashed line (1), to normalise US dollars to 1959 dollars, up to 2020. So $1 in 1959 inflates according to the exponential red curve (1) in Chart 2. Because the M2 currency supply after 2020 departs strongly from the exponential in Chart 1 we have piecewise separately modelled the M2 money supply between 2020 and 2024 using the blue polynomial curve (2). This is to compensate for the absolutely unprecedented additional currency flooded into the market from the COVID period. Due to QT in 2023 curve (2) is now approaching the theoretical value of curve (1) in late 2023.
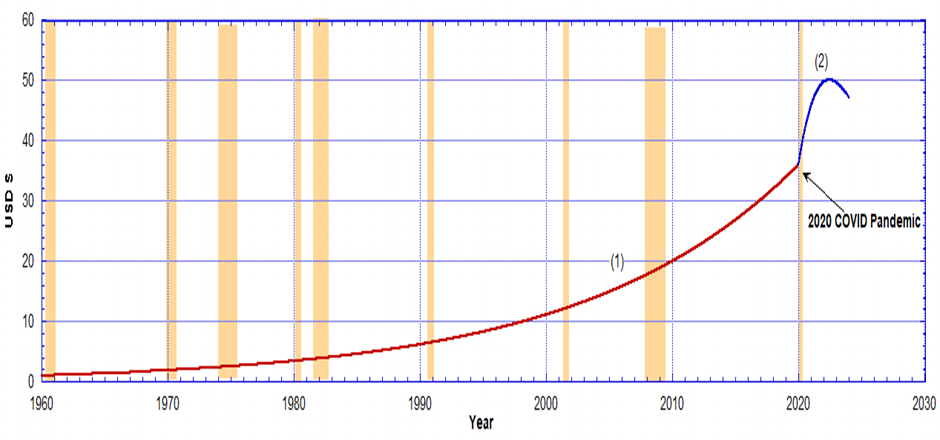
Chart 2: $1 in 1959 will deflate by the exponential (red) curve followed by the blue curve (2) as shown. This is the price inflation of 1/35 oz of gold over this time period resulting only from the expansion of the M2 currency supply. Thus the gold price is inflated by a factor of 47 by the end of 2023 in terms of current dollars. This means that the USD has lost about 98% of its value in the last 65 years. If the price of gold remains constant in terms of 1959 dollars then its current price is only rising due to inflation. However after 2020 the anomalous curve (2) had to be used to allow for the massive additional deflation of the dollar’s value in that period.
Using the curves (1) + (2) for normalised 1959 dollars, from Chart 2, we have plotted in Chart 3 the normalised price of gold as a function of time in years from 1959 to December 2023. By dividing the price of an ounce of gold by the dollar inflation factor from Chart 2, we get the price of an ounce of gold in 1959 dollars. As a result we have the price of gold over 65 years priced in 1959 dollars. The color-coding for the red and blue data is merely maintained to show the respective periods where either red curve (1) or the blue curve (2) has been used to calculate the gold price in 1959 dollars.
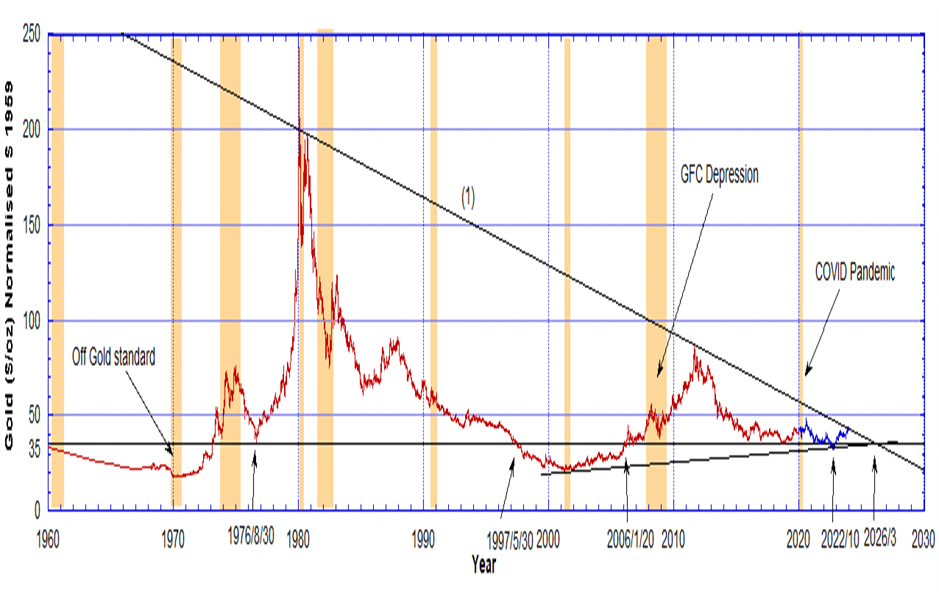
Chart 3: The price of an ounce of gold in 1959 dollars. The red data are the price of gold ($/oz) scaled by the USD normalisation curve from Chart 2 using curve (1) and the blue data are scaled using curve (2).The historical gold price data were downloaded from Auronum, the National Mining Association and YCharts. The horizontal solid line is the $35 price for an ounce of gold from 1959. The descending solid straight line (1) touches the tips of the peaks except in 1980 where a few points break above it. The bottom ascending solid line, in two places, touches the minimal gold price and also coincides with the same apex point in 2026. The sepia strips indicate recessions.
Before 1970 we were on the gold standard and the price of gold was essentially constant while currency was being created. Therefore, using 1959 dollars we notice the price of gold was falling in real terms, despite rising slightly in inflated dollar terms. No wonder the US government had to close the gold window, as foreign central banks were taking advantage of the low gold price and getting rid of dollars.
After 1971 President Nixon uncoupled the dollar from a fixed amount of gold and thus the real price of gold, in 1959 dollar terms, began to rise very significantly until it peaked in 1980. There was a brief period when it dipped back and nearly touched the $35 price in August 1976 but exploded upward after that.
Because Charts 3 and 4 use dollars of constant gold value (i.e. 1/35 oz of gold in 1959) we can compare the ‘real’ gold price, which could be seen as its purchasing power, over these decades. Generally, one can observe a fall in the real gold price during any recession as indicated in the sepia strips.
By June 1997 the gold price fell back to $35 (1959 dollars), dropped below $35 and stayed below it until January 2006. That was a good time to buy gold, as it was cheap. It peaked again by August 2011 and around October 2022 dropped below $35 for 2 months but now appears to be converging on an apex point of $35 in 2026. The price rally peaks have been diminishing as a function of time.
We can see recent features more clearly if we look at the same data but from 2005 onwards, as shown in Chart 4.

Chart 4: The price of an ounce of gold in 1959 dollars. These are the same data as Chart 3 but only data after 2005 are shown. The horizontal solid line is the $35 price of an ounce of gold from 1959. The descending solid straight line (1) touches the tips of the peaks and was derived in Chart 3. The sepia strips indicate recessions.
Here we have a picture of the gold price in 1959 dollars where blue data are the result of the 2020 QE4 credit expansion. The gold price met resistance along the straight line (1) (see Chart 3) in a descending triangle formation. After 2006 the price has remained above $35 except around October 2022.
What is most important is that as of the end of December 2023 it looks like the real price is about to break above line (1). This is the limit of the currently available data though. If this happens it would be the first time since 1980 this line has been broken through. That means the gold price has increased in real terms above the statutory $35 from where the inflationary era really kicked off.
Any value above the horizontal $35 line is an increase in real terms. But to break out above line (1) seems to mean breaking through some notional resistance and it signals more buyers entering the market.
Are we on the verge of such a breakout?
If the Fed starts the presses again in 2024 causing greater price inflation, the price of gold in current dollars has to explode to keep the price in 1959 dollars within the triangle in Chart 4. But all indications are the markets will ignore them and the real price will explode above the resistance line (1) in Chart 4 as the price of gold breaks out of these restraints like it did in 1980. That means a price increase in real terms. The question is, how high does the real price of gold have to go to inspire global dollar rejection and remonetization of money itself?


