RESUMEN: Siempre que los gestores de riesgos se enfrentan a una profunda incertidumbre y a una complejidad organizada, los métodos de inferencia probabilística que exigen entradas sólidas y resultados precisos no pueden utilizarse de manera eficaz. Esta es una tesis de este artículo que derivamos desde un punto de vista sistémico y que discutimos en el contexto de la praxeología. Más específicamente, nuestra contribución a la literatura de la Economía Austriaca es doble. En primer lugar, después de revisar la nomenclatura knightiana de riesgo contra la incertidumbre, que según Hoppe (2007) es similar al trabajo de Ludwig von Mises sobre el tema, presentamos nuestra propia concepción del riesgo que difiere de su noción. En segundo lugar, seguimos a Hoppe (2007) en la evaluación de los argumentos de Knight y Mises contra la posibilidad de aplicar la teoría de la probabilidad en el área de la acción humana, pero llegamos a una conclusión diferente y más matizada. En particular, esbozamos un caso que parte caminos con el enfoque praxeológico.
PALABRAS CLAVE: Economía austriaca, riesgo, incertidumbre, complejidad, probabilidad
CLASIFICACIÓN JEL: B4, C1
El Dr. Christian Hugo Hoffmann (choffmann@ethz.ch) es postdoctorado en la Cátedra de Riesgos Empresariales del Instituto Federal Suizo de Tecnología de Zurich (ETH), Suiza.
Quarterly Journal of Austrian Economics 21, no. 3 (Otoño 2018) número completo, haga clic aquí.
Sin embargo, ya es hora de que nos tomemos más en serio nuestra ignorancia.
– (Friedrich A. Hayek, 1967)
1. INTRODUCCIÓN
Este artículo caracteriza y discute diferentes conceptos de riesgo y busca definir un significado apropiado del término en el ámbito de la economía y las finanzas. El objetivo no es sólo profundizar en nuestro conocimiento conceptual, sino también, y esto es particularmente relevante para el austriaco, identificar y examinar el potencial de ir más allá de la mera y rígida dicotomía riesgo contra incertidumbre en la que se basan Knight y Ludwig von Mises. Esto se logra explorando si y en qué medida la sistematización puede considerarse posible en el ámbito no probabilístico de la incertidumbre. Aunque al final también diferenciaremos entre riesgo e incertidumbre knightiana (por así decirlo), es importante señalar que sólo apoyamos un único concepto de riesgo que es diferente del riesgo knightiano y que será bautizado como Riesgo I (sección 5). Introducimos el Riesgo I de manera deductiva postulando cuatro requisitos que debe cumplir una noción de riesgo (sección 4). Antes de eso, revisamos la literatura (sección 2) y ponemos el foco en el ángulo de riesgo de Knight y Mises (sección 3). Cerramos este documento en las secciones 6 y 7 donde detallamos las lecciones de la taxonomía del riesgo que estamos proponiendo para el austriaco.
La ausencia de una definición aceptada y apropiada del riesgo en la literatura no es simplemente una cuestión académica abstracta de la torre de marfil. Por ejemplo, los riesgos en y para los sistemas económicos y financieros se consideran desencadenantes de las crisis financieras mundiales (Schwarcz, 2008, págs. 193 a 249; Kelly, 1995, págs. 221 y ss.). Tener definiciones claras es un requisito fundamental para la gestión y el modelado (Fouque y Langsam, 2013, p. xxviii). Sin una noción bien pensada de riesgo (financiero) y enfoques para medir y gestionar la cantidad y la naturaleza de los riesgos, sería difícil dirigir eficazmente las acciones indispensables (por ejemplo, la mitigación) sin correr el riesgo real de hacer más daño que bien.
2. LA NOCIÓN DE RIESGO EN LA LITERATURA
En contextos no técnicos y contextos de lenguaje común, la palabra «riesgo» se refiere, a menudo de manera bastante vaga, a situaciones en las que es posible pero no seguro que ocurra algún evento indeseable (Hansson, 2011; Heinemann, 2014).1 Más precisamente, el filósofo Sven O. Hansson distingue cinco usos y significados del término particularmente importantes y más especializados, que se utilizan ampliamente en todas las disciplinas académicas y/o en el lenguaje cotidiano (Hansson, 2011).
(1) riesgo = un evento no deseado que puede o no ocurrir.
Un ejemplo de este uso es: «El riesgo de un colapso financiero es enorme».
(2) riesgo = la causa de un evento no deseado que puede o no ocurrir.
Un ejemplo de este uso es: «Los préstamos subprime son un riesgo importante para el surgimiento de una burbuja inmobiliaria». Tanto (1) como (2) son sentidos cualitativos de riesgo. La palabra también tiene significados cuantitativos, de los cuales el siguiente es el más antiguo:
(3) riesgo = probabilidad de que ocurra un evento no deseado que puede o no ocurrir.
Este uso se ejemplifica en la siguiente declaración: «El riesgo de que ocurra un colapso financiero en los próximos cinco años es del 70%».
(4) riesgo = el valor de la expectativa estadística de un evento no deseado que puede o no ocurrir.
El valor de expectativa de un posible evento negativo es el producto de su probabilidad y de alguna medida de su gravedad. Es común utilizar el monto total de los costos monetarios como una medida de la gravedad de un choque financiero. Con esta medida de severidad, el «riesgo» (en el sentido 4) cargado con un colapso financiero potencial es igual al número estadísticamente esperado de costos monetarios; es decir, por ejemplo, 70% (basándose en el ejemplo de (3)) veces USD 10T resulta en USD 7T de los costos totales esperados de una crisis financiera global. Otras medidas de gravedad dan lugar a otras medidas de riesgo.2
(5) riesgo = el hecho de que una decisión se toma en condiciones de probabilidades conocidas («decisión bajo riesgo» en lugar de «decisión bajo incertidumbre»).3 Véase la nota 28 para un ejemplo.
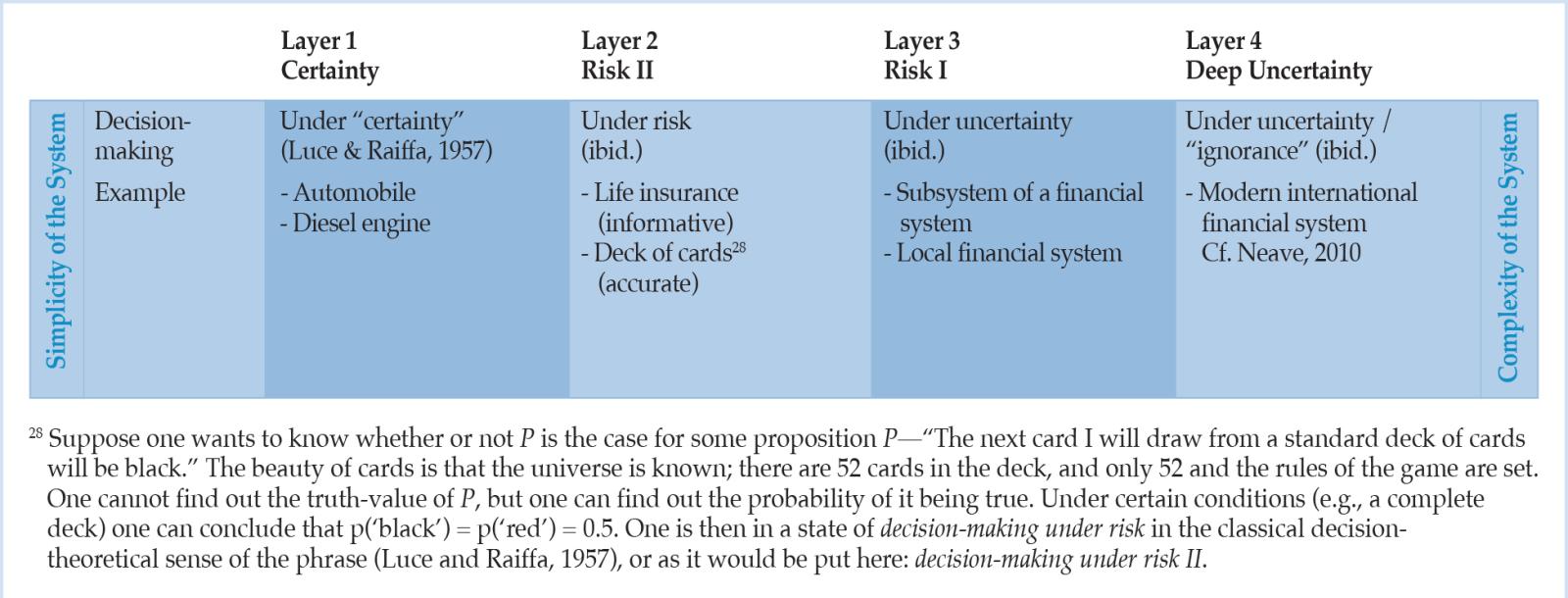
Todos los conceptos de riesgo tienen en común lo que los filósofos llaman contingencia, la distinción entre eventos posibles y reales o acciones posibles y elegidas (Renn, 2008, p. 1). Además de estos cinco significados comunes de «riesgo», según Hansson (2011), existen otros significados más técnicos, que están bien establecidos en campos especializados de investigación. Con respecto a los análisis económicos y particularmente relevantes para los fines de este estudio, no es de extrañar que el debate actual sobre el riesgo se asemeje a una confusión de lenguas babilónicas. La situación actual se caracteriza por muchos conceptos poco justificados e incoherentes sobre el riesgo (Aven, 2012, p. 33). Algunas de las muchas definiciones diferentes que están circulando están truncadas y en la Tabla 1 se presenta un sistema de subsunción de las mismas. El propósito de este resumen es exponer la variedad de nociones de riesgo material, en lugar de afirmar que las categorías proposiciones son exhaustivas o mutuamente excluyentes.
Tabla 1: Sistema de clasificación de las definiciones de riesgo y caracterización de las diferentes categorías de definición de riesgo.4
Tabla 1: Sistema de clasificación de las definiciones de riesgo
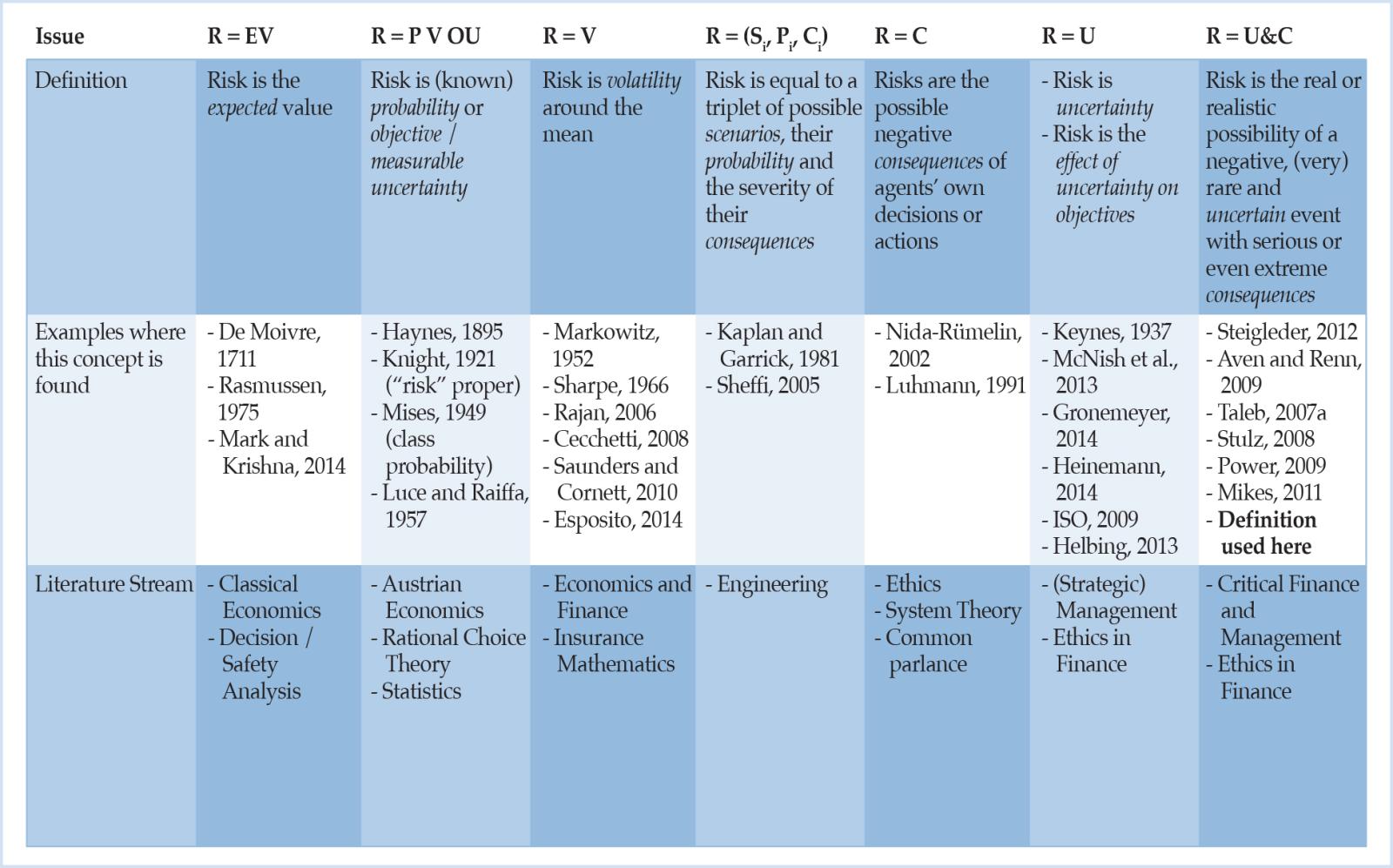
Tabla 1 Sistema de clasificación de las definiciones de riesgo 2
A la luz de esta ambigüedad, la siguiente sección presta especial atención a cómo el término «riesgo» ha sido acuñado por la escuela austriaca de economía, por Ludwig von Mises y Frank Knight en particular.
3. LA NOCIÓN DE RIESGO EN EL AUSTRIANISMO
Hoppe (2007) merece reconocimiento por investigar una similitud sistemática, aunque rara vez notada, en las obras de Knight (1921) y Mises (1949), concretamente en términos de su postura sobre el riesgo, la incertidumbre y (el alcance de) la (teoría de la) probabilidad.5 Sin embargo, la similitud concierne más de lo que él dice. La conclusión de Hoppe no es lo suficientemente satisfactoria porque permanece incompleta cuando simplemente observa que tanto Knight como Mises comparten una visión crítica similar sobre las limitaciones de la teoría matemática de la probabilidad, que no resultaría útil en nuestros esfuerzos diarios de predecir la acción humana (Hoppe, 2007, p. 19). Dejando eso por el momento, Hoppe no discute una intrigante deficiencia de la que adolecen ambas obras. Knight (1921, cap. 7 y 8) y Mises (1949, cap. 6) tratan las nociones de incertidumbre y probabilidad, que son una preocupación primordial de la praxeología, pero ambos tratamientos carecen de cierta claridad conceptual. Para ser precisos, no estamos en desacuerdo con la actitud crítica de Hoppe o de Knight/Mises hacia la aplicabilidad de la teoría de probabilidad numérica o kolmogoroviana. Más bien, la mencionada falta de claridad conceptual sobre las nociones de riesgo se refiere a una identificación ingenua del riesgo con (una interpretación de la frecuencia de) la probabilidad a la que sucumben tanto Knight como Mises y que no es evaluada críticamente por Hoppe.
Knight (1921, págs. 223 y ss.) detecta probabilidades empírico-estadísticas y las define como contingencias «asegurables» o «riesgo». Mises está de acuerdo con él (Hoppe, 2007, p. 11). Sin embargo, ¿por qué este enfoque es ingenuo? En la sección 4 lo llamaremos problemático porque no cumple con el primero, segundo y tercero de los cuatro requisitos que vamos a establecer en relación con un concepto adecuado de riesgo. Además, la interpretación de la frecuencia de la probabilidad misma está cargada de inconsistencias (cf. Hájek, 2011 para una sinopsis). Por lo tanto, al anticipar el razonamiento que subyace a los criterios 1 a 3 de la sección 4 y al señalar las objeciones al frecuentismo en la literatura, estamos justificados para afirmar la primera de dos brechas en la investigación.
Brecha de investigación I: Mala conceptualización del término «riesgo» y conocimiento de las relaciones conceptuales entre «riesgo», «incertidumbre» y «probabilidad» en un contexto financiero y económico.
Mises (1949, págs. 107 y ss.) ni siquiera señala el «riesgo» como terminus technicus en este contexto de elaboración de las interpretaciones de la probabilidad. En cambio, primero comenta de manera bastante vaga:6
Una declaración es probable si nuestro conocimiento sobre su contenido es deficiente. No sabemos todo lo que se requeriría para una decisión definitiva entre lo verdadero y lo no verdadero. Pero, por otro lado, sí sabemos algo al respecto; estamos en condiciones de decir algo más que simplemente non liquet o ignoramus. (Mises, 1949, p. 207).
Dentro de esta amplia, general y subdeterminada clase de afirmaciones probabilísticas, Mises distingue entonces dos subclases categóricamente distintas. La primera probabilidad, entendida en sentido estricto y que permite la aplicación del cálculo de probabilidad, lleva la firma de su hermano Richard, quien ante todo acuñó el concepto objetivo de probabilidad (Mises, 1939), y se denomina «probabilidad de clase»:7
La probabilidad de clase significa: Sabemos o suponemos saber, con respecto al problema en cuestión, todo sobre el comportamiento de toda una clase de eventos o fenómenos; pero sobre los eventos o fenómenos singulares reales no sabemos nada más que que que son elementos de esta clase. (Mises, 1949, p. 207).
Por otro lado, Knight (1921, pp. 223f., 226, 231f.) llama al otro tipo de contingencia (es decir, probabilidades que no son a priori ni empírico-estadísticas) «verdadera incertidumbre» y la describe como una estimación o juicio intuitivo. Por ejemplo, las decisiones de las empresas «se refieren a situaciones que son demasiado singulares, en términos generales, para que cualquier tipo de tabulación estadística tenga valor orientativo. La concepción de una probabilidad o azar objetivamente medible es simplemente inaplicable». (Knight, 1921, p. 231). Casi tres décadas después, Mises (1949, p. 110) añade que la verdadera incertidumbre o probabilidad de caso, que es como él se refiere a ella, significa:
Sabemos, con respecto a un acontecimiento en particular, algunos de los factores que determinan su resultado; pero hay otros factores determinantes de los que no sabemos nada. La probabilidad de un caso no tiene nada en común con la probabilidad de una clase, pero sí con lo incompleto de nuestro conocimiento. En todos los demás aspectos, los dos son completamente diferentes. (Mises, 1949, p. 110).
En particular, mientras que el cálculo de probabilidad sólo es aplicable a clases o colectivos «genuinos» (de ahí el nombre de probabilidad de clase), la probabilidad de caso se refiere a casos/eventos individuales, únicos y no repetibles «que como tales —es decir, con respecto al problema en cuestión— no son miembros de ninguna clase» (Mises, 1949, p. 111). Por lo tanto, quedan fuera del alcance de la teoría clásica de la probabilidad. Sin embargo, ¿qué tipo de eventos deben ser considerados como instancias de probabilidad de caso según Mises? Proporciona al lector la siguiente respuesta inicial:
El campo de aplicación de la primera[clase o frecuencia de probabilidad] es el campo de las ciencias naturales, totalmente regido por la causalidad; el campo de aplicación de la segunda[caso de probabilidad] es el campo de las ciencias de la acción humana, totalmente regido por la teleología. (Mises, 1949, p. 107).
De ello se deduce que «la acción humana es la fuente de la incertidumbre “verdadera”, no cuantificable (knightiana)» (Hoppe, 2007, p. 11). Compartimos la observación de Hoppe de que, desafortunadamente, Mises (1949) es menos que franco al dilucidar por qué las acciones (elecciones) humanas son intratables por la teoría de la probabilidad (en la interpretación de la frecuencia) (ibíd.). Además, sin embargo, afirmamos que la contribución principal que Hoppe pretende hacer en su trabajo, a saber, hacer que la razón por la que las opciones son intratables por la interpretación de la frecuencia de la probabilidad sea explícita basada en el marco de Mises, es insuficiente, y que proporciona pruebas en la sección 6. En pocas palabras, no aceptaremos la lógica de Hoppe porque rechazamos el marco de Mises para este propósito en particular. En su lugar, presentaremos la Proposición II y, por lo tanto, basaremos el asunto del alcance y las limitaciones de la teoría de la probabilidad en cuestiones de complejidad en lugar de la acción humana. Por ahora, reconocemos
Brecha de investigación II: Falta de comprensión de por qué la acción y las opciones humanas están fuera del alcance de la teoría clásica de la probabilidad (kolmogoroviana).
A continuación, abordamos estas dos lagunas en la investigación. La Sección 6 busca cerrar la brecha de investigación II, aunque la proposición de que la acción humana per se no puede ser capturada por las estadísticas de probabilidad resulta ser insostenible. La sección 5 se centra en la brecha de investigación I y el capítulo siguiente constituye un paso necesario en esta dirección. Dicho de otra manera, algunas notas sobre la epistemología del riesgo son en primer lugar para escapar de las posibles trampas antes de deducir nuestra propia definición de riesgo.
4. LA EPISTEMOLOGÍA DEL RIESGO
Cuando hay un riesgo, debe haber algo que se desconoce o que tiene un resultado desconocido. Por lo tanto, el conocimiento sobre el riesgo es el conocimiento sobre la falta de conocimiento (Hansson, 2011). Esta combinación de conocimientos y la falta de los mismos contribuye a dificultar la comprensión de las cuestiones de riesgo desde un punto de vista epistemológico.
En segundo lugar, es sensato reconocer que el riesgo no se refiere simplemente a algo desconocido, sino a dibujar un marco conceptual que distinga entre lo conocido, lo desconocido y lo incognoscible («KuU», tal como lo denomina Diebold et al., 2010). Por consiguiente, Kuritzkes y Schürmann (2010, p. 104) llaman riesgo conocido (K) si puede ser identificado y cuantificado ex ante; desconocido (u) si pertenece a un colectivo de riesgos que puede ser identificado pero no cuantificado de manera significativa en la actualidad;8 e incognoscible (U) si la existencia del riesgo o conjunto de riesgos no es previsible, y mucho menos cuantificable, ex ante. Nota bene: no hay que trazar una clara línea de definición entre estas clases, tal vez dejando las clases KuU a lo largo de un continuo de conocimientos.
En tercer lugar, las cosas son aún más confusas porque incluso los riesgos «conocidos» (en el sentido de Kuritzkes y Schürmann, 2010) contienen incertidumbre: «[...] como muestra dolorosamente la evidencia reciente procedente de los mercados financieros, la opinión según la cual una “distribución de probabilidad conocida” no contiene incertidumbre no es del todo correcta» (Fedel et al., 2011, p. 1147).9 Los autores refuerzan su afirmación de la siguiente manera (Fedel et al., 2011, p. 1147): Suponga que se está tirando un dado. Una cosa es estar inseguro sobre la cara que eventualmente aparecerá (un riesgo «conocido»). Una cosa muy diferente es no saber si la muerte es justa o imparcial (¿se conoce realmente el riesgo aparentemente conocido?) (Fedel et al., 2011, p. 1147). En otras palabras, podemos diferenciar naturalmente entre incertidumbre de primer orden e incertidumbre de segundo orden, respectivamente. En el primer caso, no estamos seguros de la situación (actualmente desconocida). En este último caso, no estamos seguros de nuestra incertidumbre, es decir, la incertidumbre de segundo orden se refiere a la evaluación que hace un agente sobre su propia incertidumbre (Fedel et al., 2011, pp. 1147f.).10
Finalmente, en cuarto lugar, Hansson (2011) observa que un problema importante en la epistemología del riesgo, problema al que se presta especial atención en este estudio, es cómo abordar las graves limitaciones que caracterizan nuestro conocimiento del comportamiento de sistemas complejos únicos que son esenciales para la estimación del riesgo (por ejemplo, los sistemas financieros modernos). Estos sistemas contienen componentes y tantas interacciones entre ellos, potencialmente cambiantes, que en la práctica resulta impredecible (Hansson, 2011).
Estos cuatro puntos ya presagian que la relación entre los conceptos de «riesgo», «conocimiento» e «incertidumbre» parece ser amplia, de múltiples niveles y esquiva. De ahora en adelante, tratamos de hacer frente a estas cuestiones y, además, establecer cuatro condiciones explícitas para definir una noción de riesgo adecuada, es decir, más útil y consistente.11
Condición 1: El riesgo debe definirse de tal manera que se pueda distinguir entre el riesgo per se (qué es el riesgo) y cómo se mide, describe o gestiona el riesgo (Aven, 2012, p. 33; Bradley y Drechsler, 2014, p. 1226).
Justificación: Esta condición es importante porque existen perspectivas sobre el riesgo en las que no se hace esta distinción (véase la Tabla 1 y véase, por ejemplo, Beck, 1992, pág. 21; Hansson, 2007, pág. 27). Al igual que MacKenzie (2006, págs. 143-179), George Soros (2008, pág. 3) observa que «nuestra comprensión del mundo en el que vivimos es inherentemente imperfecta porque somos parte del mundo que tratamos de comprender» y se centra en «cómo nuestro conocimiento del mundo es interdependiente de nuestras mediciones del mismo» (Blyth, 2010, pág. 460).12 En principio, todas las herramientas (de medición o descripción o de gestión) que se utilizan (que podrían estar basadas en modelos estocásticos) deben tratarse como tales. Toda herramienta de este tipo tiene sus limitaciones, a las que debe prestarse la debida atención. Al distinguir entre el riesgo como concepto y sus descripciones o valoraciones «buscaremos más fácilmente lo que falta entre el concepto general y la herramienta» (Aven, 2012, p. 42). Del mismo modo, si no se establece un marco adecuado que aclare la disparidad entre el concepto general de riesgo y la forma en que se está midiendo u operando, etc., es difícil saber qué buscar y cómo mejorar estas herramientas (Aven, 2012, p. 42). Además, es un principio central de la ciencia de sistemas, que a su vez está en consonancia con la línea de pensamiento austriaca,13 examinar las cuestiones desde múltiples perspectivas —«ampliar los límites de nuestros modelos mentales» (Sterman, 2000, p. 32)— y, en consecuencia, el concepto de riesgo no debe ser iluminado por una sola perspectiva teórica (por ejemplo, meros fundamentos probabilísticos); no debe basarse en una sola herramienta de medición. Porque en los diversos entornos científicos, áreas de aplicación o contextos específicos, podría no haber una mejor manera de medir/describir el riesgo. Esta parece ser, por lo tanto, una premisa razonable y no controvertida que puede reforzarse aún más mediante una analogía con el debate austriaco sobre el concepto único de «utilidad» que se ha puesto en práctica de diferentes maneras. Un campo alrededor de Böhm-Bawerk mantendría una comprensión cardinal de la utilidad, es decir, que la utilidad de los bienes puede medirse y expresarse como un múltiplo de una unidad. Por el contrario, Čuhel, Mises, y muchos más defenderían una comprensión ordinal de la utilidad (Moscati, 2015). Así, una vez que permitimos la distinción entre utilidad y su medición, permitimos que ambas partes, y potencialmente otras, hablen del sentido de la utilidad desde diferentes ángulos, elaboren diferentes facetas de la noción amplia, y así sucesivamente (ya sea que se trate de una función de utilidad cardinal o de una comprensión ordinal).
Aplicación al marco Knightiano/Misesiano: Cuando Knight (o Mises) identifica el riesgo con (una interpretación de la frecuencia de) la probabilidad, no pasa esta prueba porque entonces no se diferencia entre la noción (es decir, riesgo y por lo tanto probabilidad) y su operacionalización (es decir, la medida de probabilidad).
La segunda condición es la siguiente:
Condición 2: El riesgo debe definirse de tal manera que se pueda distinguir entre lo que es el riesgo y cómo se percibe el riesgo (Aven, 2012, p. 34),14 así como que la definición no presuponga una interpretación del riesgo objetivo o subjetivo (Hansson, 2011).
Justificación: Existe un importante debate entre los profesionales del riesgo sobre la naturaleza de los riesgos: son los riesgos construcciones sociales o subjetivas de (ideas humanas sobre la realidad, una característica del estado de información del agente) o los fenómenos reales y objetivos (representaciones de la realidad, una característica del mundo mismo;). Willett (1901) y Hansson (2011), por ejemplo, defienden un fuerte componente objetivo del riesgo: «Si una persona no sabe si la serpiente de pasto es venenosa o no, entonces está en un estado de incertidumbre con respecto a su capacidad para envenenarla. Sin embargo, como esta especie no tiene veneno, no hay riesgo de envenenamiento» (Hansson, 2011). Por otra parte, es obvio para otros que los riesgos constituyen modelos mentales (Renn, 2008, p. 2). No son verdaderos fenómenos, sino que se originan en la mente humana (Renn, 2008, p. 2). Como señala Ewald (1991, pág. 199): «Nada es un riesgo en sí mismo; no hay riesgo en la realidad. Todo puede ser un riesgo; todo depende de cómo se analice el peligro, cómo se considere el evento». El marco de definición debería, por lo tanto, tratar de «evitar el realismo ingenuo del riesgo como categoría puramente objetiva, así como la perspectiva relativista de hacer que todos los juicios de riesgo sean reflejos subjetivos del poder15 y de los intereses» (Renn, 2008, p. 3).
Aplicación al marco Knightiano/Misesiano: No es necesario reafirmar las bien conocidas objeciones a las probabilidades objetivas (por ejemplo, cf. Hájek, 2011 para una visión general), pero, curiosamente, dado que Knight y Mises adoptan una noción de probabilidad basada en el frecuentismo, también parecen respaldar una interpretación puramente objetiva del «riesgo». Por lo tanto, su marco tampoco pasa esta segunda prueba. Por lo menos, se necesitaría alguna aclaración más porque, por otro lado, el subjetivismo se considera un pilar central para los economistas de la Escuela Austriaca (por ejemplo, Spitznagel, 2013, págs. 21, 76). O tal vez simplemente se deduce entonces que una posición agnóstica debería ser tomada como lo sugiere la Condición 2.
Hay por lo menos dos requisitos más para una buena definición de riesgo.
Condición 3: El riesgo debe definirse de tal manera que ayude a la persona que toma las decisiones en lugar de inducirla a error en muchos casos (Aven, 2012, p. 42) y, por lo tanto, la definición del riesgo debe captar las principales intuiciones preteóricas sobre el riesgo (Rothschild y Stiglitz, 1970, p. 227).
Justificación: A primera vista, esta condición puede parecer trivial, pero no hay que olvidar que el riesgo no puede limitarse a la torre de marfil de las deliberaciones académicas. Aunque se trate de un concepto teórico y abstracto, el riesgo ha forjado un vínculo directo con la gestión de los desafíos de la vida real y la toma de decisiones reales. Tiene un impacto directo en nuestra vida y la orientación hacia la toma de decisiones y la acción humana es también clave para el austriaco (Mises, 1949). En el contexto bancario, los bancos, los contribuyentes y los gobiernos perdieron mucho dinero (y mucho más; por ejemplo, credibilidad) porque los gestores de riesgos (en un sentido amplio) ignoraron o juzgaron mal los riesgos, calcularon mal las incertidumbres o tuvieron demasiada confianza en su capacidad para dominar situaciones peligrosas (FCIC, 2011). En última instancia, sólo el tiempo y la retroalimentación de la práctica económica pueden decir si esta premisa se cumple o no.
Aplicación al marco Knightiano/Misesiano: Algunas proposiciones como la de R = P V OU, es decir, el marco de Mises, 1949 y Knight, 1921 (ver Tabla 1), no cumplen este criterio porque, en palabras de Aven (2012, p. 41), «referirse al riesgo sólo cuando tenemos distribuciones objetivas significaría excluir el concepto de riesgo de la mayoría de las situaciones de interés». Por lo tanto, este concepto de riesgo no resultaría útil en muchos o la mayoría de los casos de toma de decisiones.
En relación con esta tercera premisa, que abre el debate a un público más amplio (es decir, no académico), también se puede observar la siguiente demanda ética.
Condición 4: El riesgo debe definirse de tal manera que no desvíe la atención de los efectos sistémicos que tienen un impacto no sólo en el actor, sino también en otros actores (Rehmann-Sutter, 1998, p. 120).
Justificación: La escuela de economía austriaca también enfatiza la importancia de los efectos sistémicos que se asocian generalmente con eventos (muy) de baja frecuencia en un espacio de alta dimensión —véase, por ejemplo, Spitznagel, 2012: «Los austríacos y el cisne: pájaros de una pluma diferente». Sin embargo, Rehmann-Sutter (1998, p. 122) va un paso más allá y lamenta el hecho de que en algunos conceptos económicos de riesgo, «sólo hay una posición personal: el que toma las decisiones», mientras que la mayoría de los riesgos no son individuales sino más bien sociales (Sen, 1986, pp. 158 y ss.), es decir, puede haber consecuencias negativas para los demás por «correr riesgos». Añade, sin embargo, que tenemos dificultades para incluir adecuadamente a aquellas otras personas (por ejemplo, los contribuyentes en nuestro contexto) afectadas por las consecuencias de la decisión (de gestión de riesgos) (de un banco) en el proceso de toma de decisiones, donde el concepto de riesgo se elabora en la realidad (Rehmann-Sutter, 1998, p. 122). «Estos otros participantes son abstractos; la atención se desvía de ellos. Estos participantes están conceptualmente ocultos» (Rehmann-Sutter, 1998, p. 122).
Aplicación: No podemos considerar esta crítica como fundamental en términos de los conceptos de riesgo económico que se tienen en cuenta en la Tabla 1, por ejemplo, la definición R = EV no implica una lectura limitada de las consecuencias. Por lo tanto, consideramos que el 4 es una condición débil que, en principio, puede cumplirse en todas las definiciones de riesgo. En otras palabras, la condición 4 se refiere más a la interpretación de la definición que a la definición de riesgo en sí misma. Sin embargo, se puede aprender una lección importante de esa advertencia, entre las que destaca la de Kristin Shrader-Frechette.
Shrader-Frechette (1991) señala el malestar que sentimos cuando utilizamos un concepto que fue elaborado para optimizar el comportamiento empresarial en un mercado impredecible para describir intervenciones en el sistema (financiero) con efectos adversos potenciales o reales para otras personas e instituciones. Lo que es prima facie racional podría secunda facie no ser racional si se adopta una visión de retroalimentación del mundo (Sterman, 2000). Dado que sólo esos riesgos entran en los procedimientos estándar de medición probabilística de riesgos que (¡directamente!) afectan a las respectivas organizaciones, gestores de riesgos o comerciantes, etc., a menudo no ven una conexión directa entre sus acciones y otros actores (Garsten y Hasselström, 2003, p. 259) o con cambios significativos en el sistema financiero o incluso en la economía global, que, en última instancia, repercuten en las propias instituciones individuales.
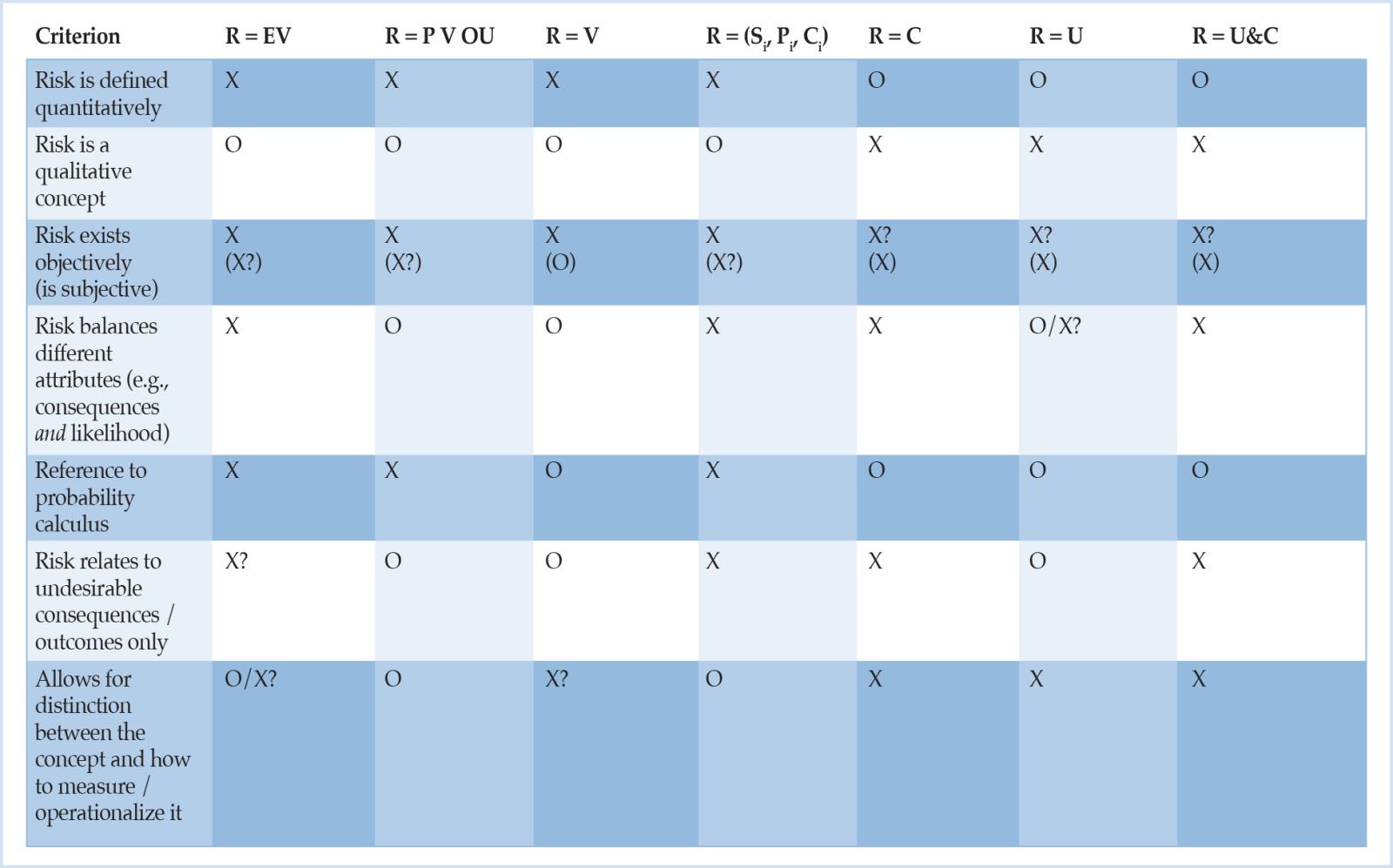
Por ahora, una primera conclusión es que, lamentablemente, muchas de las definiciones de riesgo existentes ni siquiera cumplen los dos primeros requisitos básicos (véase el Tabla 1, filas 3 y 7). En términos de la Tabla 1, sólo el riesgo en el sentido de incertidumbre (R = U) y el riesgo como la posibilidad real o realista de un evento negativo, (muy) raro e incierto con consecuencias graves o incluso extremas (R = U&C) permanecen en el juego. Dado que ver el riesgo como incertidumbre puede considerarse un caso especial de U&C, este último parece ser el candidato más prometedor, mientras que los otros conceptos de riesgo presentados no sólo no tienen algunas propiedades deseables, sino que también sufren de otras deficiencias. Por ejemplo, la identificación de riesgo con volatilidad o la variación de los rendimientos (R = V), especialmente en el contexto bancario, es claramente insatisfactoria: «Podemos construir distribuciones que tengan idéntica varianza pero con las que asociaríamos grados muy diferentes de “peligrosidad” — y riesgo, como dice el refrán, es una palabra pero no es un número» (Rebonato, 2007, p. 237; cf. también Rootzén y Klüppelberg, 1999); «[e]n todo caso, cualquiera que busque un solo número para representar el riesgo está invitando al desastre» (Taleb et al., 2009, p. 80; cf. también Power, 2007, p. 121).
Antes de que arrojemos algo más de luz sobre la U&C, tiene sentido examinar primero más de cerca otro ejemplo, a saber, el campo de la definición de riesgo R = P V OU, donde Mises (1949) y Knight (1921) hicieron una de las primeras distinciones a gran escala entre riesgo e incertidumbre, para lo que se conoció como «riesgo Knightiano» (= incertidumbre mensurable) e «incertidumbre Knightiana». Aunque puede haber buenas razones para considerar que el argumento original de Knight para distinguir entre riesgo e incertidumbre se desvía (véase la condición 3),16 es importante tenerlo en cuenta por varias razones.
En primer lugar, es muy desconcertante ver cómo diferentes economistas, expertos en riesgos y otros han reaccionado a la obra de Knight, cómo la interpretaron y qué conclusiones se han sacado. Un buen ejemplo es que mientras que tanto la comunidad financiera crítica (por ejemplo, Stout, 2012; Bhidé, 2010; Aven y Renn, 2009; Power, 2007; o Taleb y Pilpel, 2004), por un lado, y la corriente dominante económica (imperialista) (Friedman, 1976; Ellsberg, 1961; Savage, 1954), por el otro, consideran que la distinción de Knight entre el riesgo y la incertidumbre es inválida debido a que su perspectiva de riesgo es demasiado estrecha, los intereses de estos dos grupos son diametralmente opuestos entre sí: Mientras que el primero rechaza las definiciones de riesgo basadas en la probabilidad («el riesgo como concepto no debe basarse en una herramienta de medición específica [como la probabilidad-C.H.]», Aven, 2012, p. 42) en favor de la incertidumbre, el segundo sostiene que el riesgo Knightiano, es decir el riesgo medido por la probabilidad, prevalecería en lugar de la «incertidumbre» («para un hombre “racional” todas las incertidumbres pueden reducirse a riesgos [porque se cree que podemos tratar a las personas como si asignaran probabilidades numéricas a cada evento concebible -C.H.]», Ellsberg, 1961, p. 645).17
En segundo lugar, la obra fundamental de Knight podría, por lo tanto, considerarse muy influyente o incluso innovadora para la historia más reciente del pensamiento económico (Heinemann, 2014, págs. 61 y siguientes; Aven, 2012, pág. 41; Esposito, 2011, pág. 32) y sentar las bases para un significado común de «riesgo» (Hansson, 2011), especialmente relevante en economía y teoría de la decisión (Luce y Raiffa, 1957). De hecho, el vínculo entre riesgo y probabilidad se considera tan fuerte que sólo unos pocos parecen cuestionarlo: «El riesgo sólo se puede encontrar en situaciones que deben ser descritas por probabilidades» (Granger, 2010, p. 32). Además, Knight (1921) introdujo una clasificación sencilla pero fundamental de los retos de información a los que se enfrenta la gestión de riesgos de los bancos, entre los riesgos de Knightian que pueden ser abordados con éxito con herramientas estadísticas (valor en riesgo, déficit esperado, etc.), y las incertidumbres de Knightian que no pueden (Brose et al., 2014, p. 369). Una buena gestión del riesgo, por lo tanto, requiere kits de herramientas que manejen tanto el riesgo como la incertidumbre de Knightian (Brose et al., 2014, p. 369).
Por lo tanto, en tercer lugar, es importante contar con un concepto de riesgo basado en modelos de probabilidad para poder participar y contribuir al discurso del riesgo si se quiere llegar a un gran número de participantes y economistas o personas interesadas en la gestión del riesgo en la banca, en particular. Sin embargo, dado que tal definición de riesgo (que será bautizada como Riesgo II) no haría justicia a los requisitos establecidos anteriormente (por ejemplo, la primera condición), no será la que se persiga y adopte en este estudio después de todo.
Por lo tanto, sería prematuro asumir simple y acríticamente la posición de Taleb y Pilpel (2004) o Aven (2012) de abogar a favor de dejar la nomenclatura Knightiana de una vez por todas. En cambio, nuestra estrategia es doble. Primero concluimos que el tipo de definiciones de Heinemann (2014), Steigleder (2012), Aven y Renn (2009), etc., son las más apropiadas antes de aprobar una noción limitada de riesgo que sea compatible con la forma en que se llevan a cabo las discusiones de riesgo.
5. COMPRENSIÓN DEL RIESGO
Como respuesta a la brecha de investigación I, el riesgo, en este trabajo, se parafrasea en términos generales como18
... la posibilidad real o realista de un acontecimiento positivo o negativo cuya ocurrencia no es segura o previsible,19 sino más o menos probable. Sin embargo, la probabilidad de que ocurra el evento positivo o negativo no tiene que ser conocida ni estar sujeta a una especificación numérica exacta.
Así, el término «riesgo» no se utiliza como antónimo de «incertidumbre», como es habitual en la teoría de la decisión, sino más bien como un concepto genérico que cubre tanto el «riesgo en un sentido más estricto» (lo que Knight, 1921, llama incertidumbre medible) como la «incertidumbre». Esto se debe a que con frecuencia carecemos de una base suficiente para determinar las probabilidades con precisión (Greenbaum, 2015, p. 165), como se aclarará más adelante.
Esta noción amplia de riesgo es designada por el Riesgo I. Estructuralmente, el riesgo en este sentido capta:
- ¿Qué puede pasar?
- Responder a esta pregunta requiere la identificación o descripción de las consecuencias o resultados de una actividad.
- ¿Es más o menos probable que suceda (en contraste con cuán probable es de que suceda)?
- La atención se dirige a eventos bastante raros o sistémicos en esta pieza por razones que se vuelven transparentes a continuación.
- Si esto sucede, ¿cuál es el impacto?
- Responder a esta pregunta requiere la evaluación de las consecuencias, que son bastante serias o incluso extremas. De lo contrario, los riesgos resultarían irrelevantes.
Por lo tanto, seguimos el llamado de Das et al. (2013, p. 715) de que la investigación sobre gestión de riesgos tendrá que profundizar «en el paso de preguntas más orientadas a la frecuencia “si” a un enfoque más orientado a la severidad “qué pasaría si”, y esto en varios niveles». En este tratado en particular, el enfoque se centra en los eventos de (muy) baja frecuencia en un espacio de alta dimensión o, en particular, en las pérdidas (monetarias) de baja frecuencia y alta gravedad por varias razones. Por ejemplo, empujar los fenómenos naturales a un extremo revela verdades que se desarrollan en circunstancias normales. Como subrayaron Johansen y Sornette (2001) y tras el filósofo del siglo XVI Francis Bacon, el atractivo científico de los acontecimientos extremos y sistémicos es que es en esos momentos cuando un sistema complejo ofrece vislumbres de la verdadera naturaleza de las fuerzas fundamentales subyacentes que lo impulsan (Johnson et al., 2012, p. 3).
Por consiguiente, la necesidad de abordar los resultados inesperados, anormales o extremos, en lugar de los resultados esperados, normales o medios, es un reto muy importante en la gestión del riesgo (McNeil et al., 2005, p. 20; Malevergne y Sornette, 2006, p. 79; Greenbaum, 2015, p. 164); porque mejorar la comprensión (de la distribución) de los valores extremos, que no pueden ser descartados como valores atípicos, ya que, de forma acumulativa, su impacto a largo plazo es dramático, es de suma importancia (Mandelbrot y Taleb, 2010).20
Benoît Mandelbrot utiliza una bonita metáfora para ilustrar (cf. también Churchman, 1968, p. 17): «Durante siglos, los constructores navales han cuidado el diseño de sus cascos y velas. Saben que, en la mayoría de los casos, el mar es moderado. Pero también saben que se producen tifones y huracanes. Diseñan no sólo para el 95% de los días de navegación cuando el tiempo es bueno, sino también para el otro 5%, cuando las tormentas soplan y se pone a prueba su habilidad». (Mandelbrot y Hudson, 2008, pág. 24). Y añade: Los gestores de riesgo y los inversores del mundo son, en este momento, como un marino que «construye su barco por su velocidad, capacidad y comodidad, dando poca importancia a la estabilidad y la fuerza». «Lanzar un barco así al otro lado del océano en temporada de tifones es hacer daño grave». (Mandelbrot y Hudson, 2008, pág. 276).
Claramente, esto no significa que los eventos de riesgo de (muy) baja probabilidad sean importantes simplemente porque tengan una probabilidad muy baja. Por ejemplo, existe cierta probabilidad de que un elefante rosado caiga del cielo. Pero tal riesgo no afecta las decisiones de gestión en los sistemas económicos y financieros (como los bancos). Los riesgos conocidos o desconocidos que importan para nuestros propósitos son, por supuesto, aquellos que, de haber sido conocidos por la alta gerencia, habrían resultado en diferentes acciones (Stulz, 2008, p. 64)-por ejemplo, el estallido de una burbuja de precios o la escalada de un conflicto político, etc.
En segundo lugar, se invoca un concepto estrecho de riesgo (Riesgo II); está básicamente circunscrito por dos variables clave, la gravedad de la consecuencia y su probabilidad de ocurrencia,21 y presupone que se conocen las consecuencias posibles/significativas y los valores correspondientes de gravedad y probabilidades.22 El Riesgo II abarca las definiciones de riesgo 3 a 523 de Hansson (2011) y puede considerarse como un caso especial y poco frecuente de la definición amplia de riesgo (Riesgo I). La Figura 1 muestra las relaciones conceptuales entre Riesgo I, Riesgo II e incertidumbre, y puede ser vista como nuestra proposición para cerrar la brecha de investigación I.
Figura 1: Dos conceptos de riesgo relevantes: El riesgo I engloba el riesgo II y la incertidumbre.24
Dos conceptos de riesgo relevantes
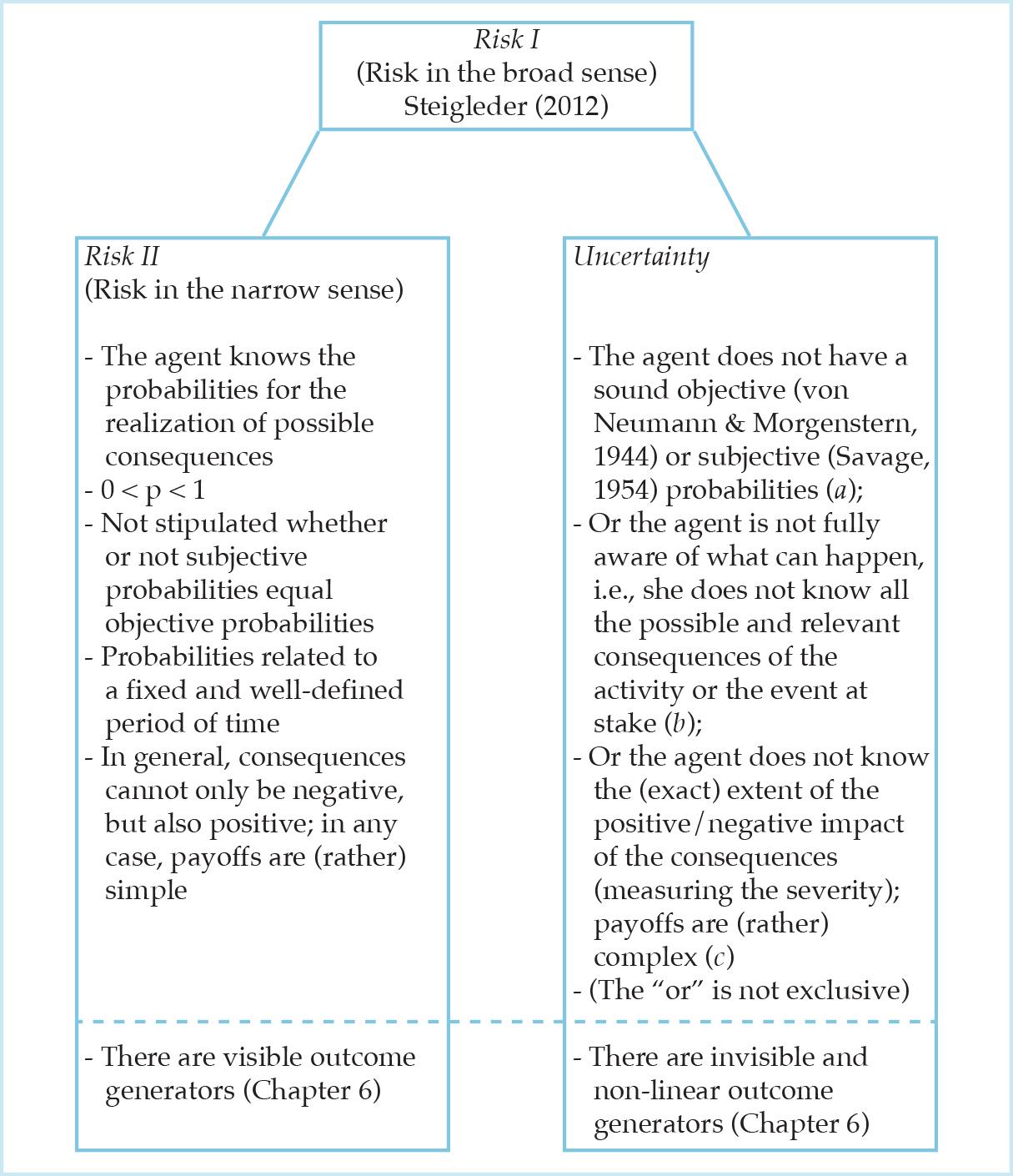
El riesgo II es más bien hipotético o una excepción y este caso se construye básicamente sólo para participar en discusiones regulares sobre el riesgo (véase más arriba, pág. 15).25 Aparte de los diferentes órdenes de incertidumbre (Fedel et al., 2011, pág. 1147; Ellsberg, 1961), se deben tener en cuenta diferentes tipos de incertidumbre. En la Figura 1, distinguimos tres tipos de incertidumbre cualitativamente diferentes: (a) lo que los teóricos de la decisión o los filósofos podrían llamar incertidumbre del estado, (b) lo que podrían llamar incertidumbre de la opción y/o incertidumbre del espacio del estado, y (c) lo que corresponde a la incertidumbre ética, una forma de incertidumbre normativa (cf. Bradley y Drechsler, 2014). Además, se discuten en la literatura muchos tipos diferentes de riesgo (riesgo empresarial, riesgo social, riesgo económico, etc., Kaplan y Garrick, 1981, p. 11) o categorías de riesgo (riesgo de mercado, de crédito, operacional, etc.) y se introducen muchos más sistemas de clasificación. Sin embargo, argumentamos que, aunque algunas de las taxonomías ofrecidas para los riesgos bancarios o para el conocimiento (o la falta de conocimiento) son persuasivas, por ejemplo, el marco conceptual «KuU» de Diebold et al. (2010), al menos el silo-tratamiento de los riesgos debería ser superado. En lugar de prestar mucha atención a las diferentes formas de riesgo, el enfoque se centra aquí en R = U&C en general. El concepto amplio de riesgo se elige como forma de descripción, ya que no está claro a priori para los riesgos concretos en cuestión si se conocen o no las probabilidades y las consecuencias potenciales, así como su gravedad. La importante distinción de Knight (Mises) entre riesgo e incertidumbre se estima separando el Riesgo II de la incertidumbre. Esta diferenciación es, en algunos casos, indispensable para el discurso del riesgo (gestión) en la banca porque surgen diferentes implicaciones: La perspectiva de riesgo elegida influye fuertemente en la forma en que se analiza el riesgo y, por lo tanto, puede tener efectos graves en la gestión del riesgo y en la toma de decisiones (Aven, 2012, p. 42). Sin embargo, gran parte de lo que hoy llamamos gestión de riesgos es «gestión de la incertidumbre» en términos knightianos, es decir, esfuerzos valientes para gestionar «objetos de riesgo» para los que los datos de probabilidad y de resultados no están disponibles o son defectuosos en un momento dado (Power, 2007, p. 26; Willke et al., 2013, p. 9).
6. UNA TAXONOMÍA DE LA INCERTIDUMBRE: ESCALAS DE MEDICIÓN Y CUANTITATIVA CONTRA CUANTITATIVA PROBABILIDADES CUALITATIVAS
Es un lugar común que no debemos emprender transformaciones inadmisibles sobre los datos que deseamos analizar, ni hacer declaraciones de intervalos sobre los datos ordinales, en particular (Flood y Carson, 1993, págs. 41 y ss.).26 Estamos de acuerdo con Mises (1949, pág. 113) en que existe una forma de incertidumbre, que él llama probabilidad de caso y nosotros llamamos incertidumbre profunda, y que no se presta a los métodos clásicos basados en la probabilidad: «La probabilidad de un caso no está abierta a ningún tipo de evaluación numérica» (Mises, 1949, p. 113). Sobre esta base, hipotetizamos que cuando nosotros, como modeladores de riesgo, estamos en un estado de profunda incertidumbre sobre algunos datos o eventos futuros, entonces podemos realizar, no un cardenal, sino una «medición» ordinal de esos riesgos solamente.27 En otras palabras, adaptada libremente de la lógica y filósofa W. V. O. Quine, el universo superpoblado de los cardenalistas ofende el sentido estético de nosotros, que tenemos gusto por los paisajes desérticos. Su aspiración a la precisión pedante es un caldo de cultivo para operaciones matemáticas desordenadas de datos y riesgos que requieren modestia.
Proposición 1: La incertidumbre profunda o probabilidad de caso no admite grados, sino que es una noción meramente comparativa.
Sin embargo, no estamos de acuerdo con Mises (1949) sobre el alcance de la probabilidad del caso vs. la incertidumbre profunda. Mientras que él afirma que «[c]ase la probabilidad es una característica particular de nuestro tratamiento de los problemas de la acción humana» (Mises, 1949, p. 111) y, por lo tanto, que la acción y las opciones humanas están fuera del alcance de la teoría clásica (kolmogoroviana) de la probabilidad, Mises se queda corto en cuanto a proporcionarnos una razón suficiente para esta afirmación (véase la brecha en la investigación II).
En cambio, nuestra estrategia es doble: Sugerimos que la clase de opciones y acciones humanas es demasiado amplia y estrecha para capturar declaraciones de incertidumbre que no pueden ser expresadas en términos probabilísticos. Es demasiado amplia porque podemos razonar probabilísticamente sobre la acción y las opciones humanas (ver «toma de decisiones bajo riesgo», Luce y Raiffa, 1957, o Tabla 1 [la columna en el centro] más abajo). Es cierto que se puede argumentar que todas las decisiones se toman «bajo incertidumbre» si uno abstrae de casos de libros de texto claros e idealizados, pero si un problema de decisión se trata como una decisión «bajo riesgo» (por ejemplo, la probabilidad de lluvia es del 70% [según el pronóstico del tiempo]; ¿debería tomar un paraguas para trabajar?) esto no significa, como aclara Hansson (2011), que «la decisión en cuestión se tome en condiciones de probabilidades completamente conocidas. Más bien, significa que se ha optado por simplificar la descripción de este problema de decisión tratándolo como un caso de probabilidades conocidas. Esta es a menudo una idealización muy útil en la teoría de la decisión» pero, al mismo tiempo, es importante distinguir entre aquellas probabilidades que pueden ser tratadas como conocidas y aquellas que son genuinamente inciertas.
La clase de opciones y acciones humanas es también demasiado estrecha porque lo que algunas (no todas) las acciones y elecciones humanas son intratables para la teoría de la probabilidad es la complejidad organizada (Weaver, 1948), como argumentamos más adelante, y la complejidad organizada caracteriza a muchos sistemas diferentes, no sólo la acción humana.
Proposición 2: La profunda incertidumbre surge de una complejidad altamente organizada y dinámica.
En un artículo clásico y masivamente referenciado, Weaver (1948) distingue tres rangos significativos de complejidad, que difieren considerablemente entre sí en el tratamiento matemático que requieren. Ofrece una clasificación que separa problemas simples, de pocas variables (o un pequeño número de factores significativos) de «simplicidad organizada» por un lado de la «complejidad desorganizada» de numerosos problemas de variables por el otro, donde las variables exhiben un alto nivel de comportamiento aleatorio. Esto deja a la «complejidad organizada» entre los dos extremos. La importancia de esta región media, sin embargo, no depende principalmente del hecho de que el número de variables involucradas sea moderado —grande en comparación con dos, pero pequeño en comparación con el número de átomos en una pizca de sal. El sello distintivo de los problemas de complejidad organizada y dinámica reside en el hecho de que estos problemas, en contraste con las situaciones desorganizadas en las que los métodos estadísticos o probabilísticos tienen la clave, muestran la característica esencial de la organización (Weaver, 1948, p. 539). Esto, a su vez, implica tratar simultáneamente un número considerable de factores que están interrelacionados para formar un todo orgánico. Las interacciones y la consiguiente interdependencia conducen a la emergencia, es decir, a la aparición espontánea de características que no pueden atribuirse al carácter de las partes individuales del sistema (Anderson, 1972) y, por lo tanto, no pueden capturarse plenamente en las estadísticas de probabilidad ni reducirse suficientemente a una fórmula simple. Se necesita algo más que el análisis matemático o las matemáticas de los promedios (Weaver, 1948, p. 540; Huberman y Hogg, 1986, p. 376).
Weaver (1948, p. 539) enumera ejemplos de problemas de complejidad organizada en los que, en cada caso, interviene un número sustancial de variables relevantes que varían simultáneamente y de manera sutilmente interconectada. En particular, se considera que lo económico, pero no sólo el ámbito de la acción humana, está dentro del ámbito de la complejidad organizada (Klir, 1991, p. 119). La Tabla 1 resume la relación entre las nociones de complejidad de Weaver y la idoneidad de los métodos estocásticos en términos del estado respectivo de las declaraciones probabilísticas. Prepara el camino para reunir el riesgo y su forma no probabilística (profunda incertidumbre), así como la complejidad, esta última como respuesta a la brecha de investigación II, en un solo esquema.
Tabla 2: Taxonomía sugerida de incertidumbres y complejidades basada en Weaver (1948).
Una taxonomía sugerida de las incertidumbres
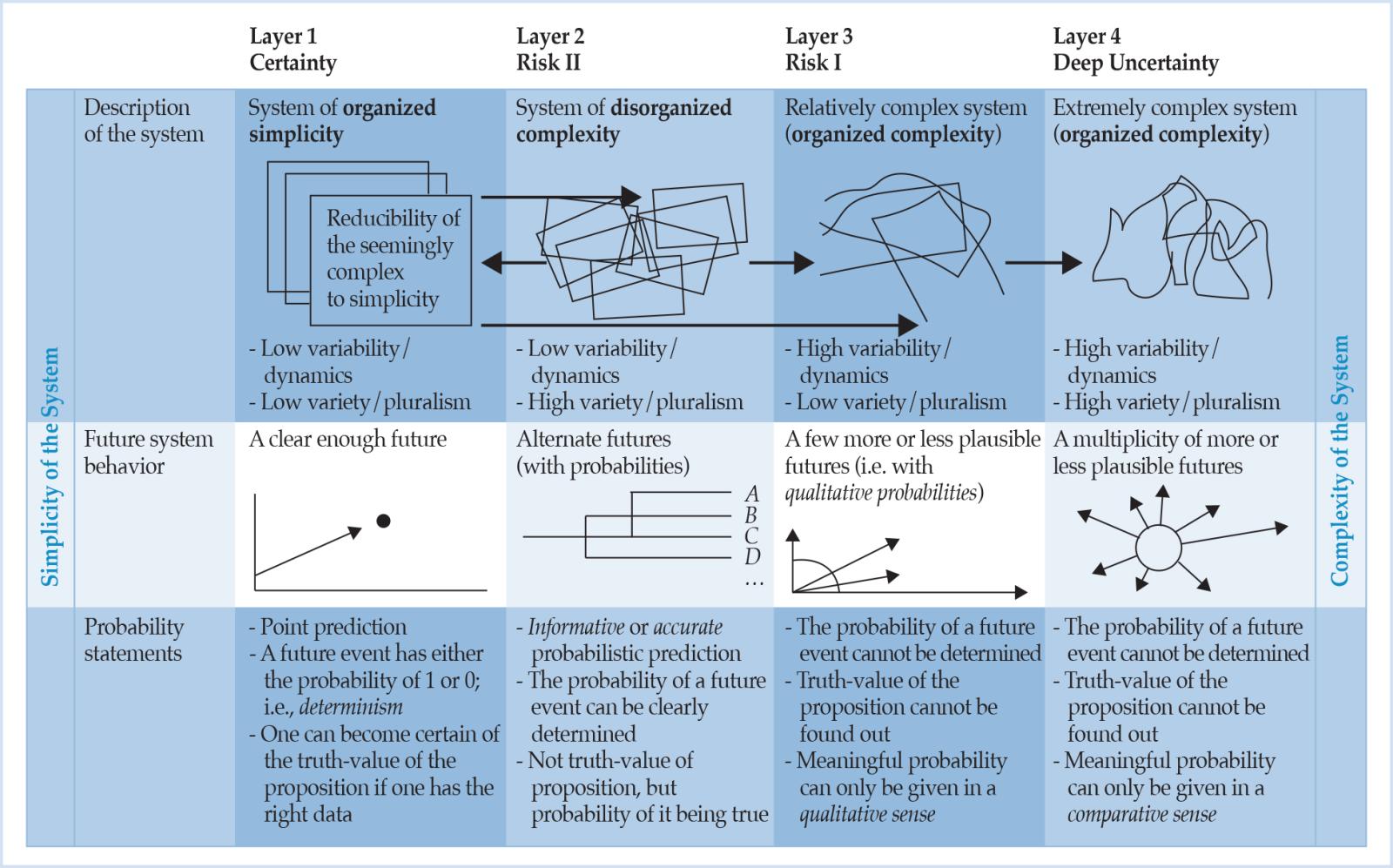
Image

7. CONCLUSIÓN
Para concluir este trabajo, la siguiente Figura 2 integra las nuevas dimensiones en torno a la incertidumbre profunda y las escalas de medición en el marco Weaveriano existente sobre el desmontaje de la noción de complejidad y en el razonamiento de Mises sobre los dos tipos diferentes de probabilidad que constituyen una subclase de incertidumbre profunda y Riesgo II, respectivamente.
Figura 2: El desmontaje de la complejidad: El marco unificador.
El desmontaje de la complejidad
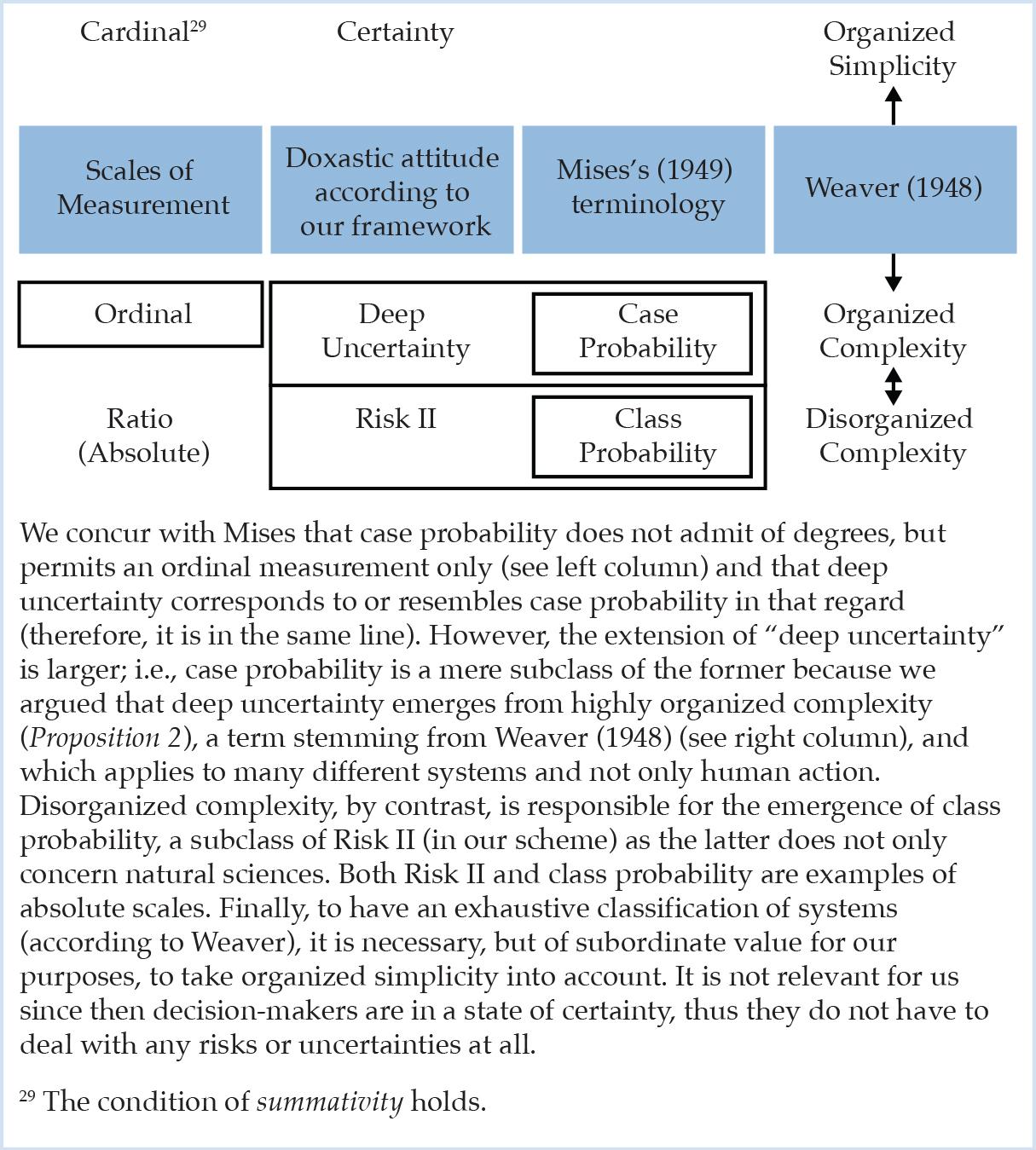
Compartimos el mismo terreno con Mises (1949) y Knight (1921) cuando somos muy cautelosos sobre el predominio de las estadísticas de probabilidad en el ámbito de la economía y las finanzas, que se caracteriza más por la probabilidad de caso, que presentamos como una noción meramente comparativa (Proposición 1), que por la probabilidad de clase. Sin embargo, muchos de los resultados de este estudio no están de acuerdo con el enfoque praxiológico. A la luz de las dos lagunas de investigación que señalamos, quisiéramos destacar dos casos:
- El «Riesgo» debe entenderse como el Riesgo I, no como el Riesgo II.
- No es la acción humana contra la no humana (o, en términos positivos, la acción humana contra las ciencias naturales, cf. Mises 1949: 107) la que decide sobre la aplicabilidad de la teoría de la probabilidad, sino el grado de complejidad organizada de un sistema en el que surge una profunda incertidumbre (Proposición 2).
Si este estudio estimula una mayor controversia sobre cómo concebir el riesgo e identificar las limitaciones de la teoría de la probabilidad, ya que tal debate se considera muy importante para el desarrollo de los campos de riesgo (Aven, 2012, p. 34), ya habrá servido a un propósito útil.
- 1El origen del concepto de riesgo no está claro. Etimológicamente, el término se deriva, entre otras cosas, de la palabra griega «rhiza», que puede traducirse con «risco», que apoya el modo negativo de explicación anterior, y de la vulgar expresión latina «risicare»/«resecare», que significa «correr hacia el peligro» o «saldar / al peligro». Véase Heinemann, 2014, p. 59.a.
- 2«Aunque los valores de expectativa se han calculado desde el siglo XVII, el uso del término “riesgo” en este sentido es relativamente nuevo. Se introdujo en el análisis de riesgos en el influyente Reactor Safety Study, WASH-1400, (Rasmussen, 1975)». (Hansson, 2011). Hoy en día, Hansson (2011) lo considera como el significado técnico estándar del término «riesgo» en muchas disciplinas. Algunos analistas de riesgo incluso piensan que es el único uso correcto del término (ibíd.).
- 3«La mayoría de las presentaciones del trabajo de la teoría de la decisión de Luce y Raiffa (1957)[basado en Knight, 1921; C.H.] distinguen clásicamente entre situaciones de certeza (cuando se conocen las consecuencias de las acciones), riesgo (cuando se conoce la probabilidad de cada una de las posibles consecuencias de una acción, pero no cuál será la real) e incertidumbre (cuando se desconocen estas probabilidades)» (Bradley y Drechsler, 2014, p. 1229).
- 4¿x: sí, o: no, x?: la respuesta según el significado de los términos o no se especifica. Un resumen similar, pero no plenamente satisfactorio, se encuentra en Aven (2012, p. 37).
- 5Sin embargo, cf. también Rothbard (1962, pp. 498-501).
- 6Una definición precisa incluye el operador lógico «si, y sólo si», que falta en el modo en que Mises introduce la «probabilidad».
- 7Además, el hecho de que Mises (1949) se muestre totalmente de acuerdo con su hermano (Mises, 1939) a este respecto, implica que utiliza deliberadamente «aleatoriamente» para referirse a «azar», lo cual es problemático (cf. Eagle, 2012).
- 8Lo desconocido podría, por lo tanto, ser también conocible en la medida en que existan (existirán) mecanismos que permitan transformar lo desconocido en conocido. Estos mecanismos pueden ser conocidos o desconocidos. A menudo se desconoce si un riesgo o circunstancia es un «desconocido conocible» o un «desconocido desconocido desconocido», lo que podría recordar al lector el dictado de Donald Rumsfeld sobre las incógnitas conocidas y desconocidas: otra línea de demarcación.
- 9Ellsberg (1961) habla de la ambigüedad de una información.
- 10En principio, son concebibles órdenes de incertidumbre aún mayores.
- 11Después de Rothschild y Stiglitz (1970, págs. 226 y ss.), es, por supuesto, imposible probar que una definición es mejor que otra. En cambio, señalan que las definiciones se eligen por su utilidad y coherencia.
- 12Un ejemplo impresionante de cómo el conocimiento está entrelazado con nuestras herramientas de medición puede ser tomado de la geometría fractal: Intuitivamente, asumiríamos que una pregunta como «¿Cuánto tiempo dura la costa de Gran Bretaña? Sin embargo, al añadir a las observaciones de Lewis Richardson (1881-1953), Mandelbrot (1967) muestra que la longitud de una línea de costa, una curva autosimilar u objeto fractal, depende de la escala a la que se mida (que se ha conocido como la «paradoja de la costa»).
- 13Por ejemplo, Mises (1949, p. 874) sitúa el aprendizaje de la economía en el contexto del pensamiento sistémico y la «interconexión de todos los fenómenos de acción» en el centro del pensamiento sistémico.
- 14Según Aven (2012), esta premisa no está en línea con la teoría cultural y el constructivismo (cf. también Jasanoff, 1999; Wynne, 1992; y comentarios críticos en Rosa, 1998). Beck (1992, p. 55), por ejemplo, escribe que «como los riesgos son riesgos en el conocimiento, las percepciones de los riesgos y los riesgos no son cosas diferentes, sino una misma cosa».
- 15El poder, por ejemplo, en la medida en que lo que cuenta como un riesgo para alguien puede ser un acto de Dios para alguien más, resignado a su destino (Bernstein, 1996b).
- 16Taleb y Pilpel (2004) y Aven (2012), por ejemplo, sostienen que debemos dejar la nomenclatura Knightian de una vez por todas: «[...] la distinción es irrelevante, en realidad engañosa, ya que, fuera de los experimentos de laboratorio, el operador no sabe de antemano si se encuentra en una situación de “riesgo Knightian”». (Taleb y Pilpel, 2004, p. 4).
- 17Sin embargo, el hecho de que el agente actúe como si la representación fuera verdadera para ella no significa que lo sea para ella. Véase Hájek, 2009, p. 238.
- 18Estos dos primeros pasajes fueron tomados de Steigleder (2012, p. 4).
- 19Seguimos a Steigleder (2012, p. 4) al llamar a un evento que se espera aquí «si se sabe que es una consecuencia normal y común de ciertas circunstancias o acciones. Siempre que un evento que es previsible en este sentido no ocurre, eso es algo anormal y necesita explicación».
- 20La necesidad de una respuesta a este desafío también se hizo evidente a raíz del caso LTCM en 1998 (McNeil et al., 2005, p. 20). John Meriwether, el fundador del fondo de cobertura, aprendió claramente de esta experiencia de turbulencia financiera extrema: «Con el aumento de la globalización, verás más crisis. Nuestra atención se centra en los extremos ahora -que es lo peor que te puede pasar en cualquier situación- porque no queremos volver a pasar por eso». (Wall Street Journal, 2000).
- 21La probabilidad de ocurrencia o al menos la probabilidad subjetiva debe ser menor que 1 y mayor que 0, de lo contrario habría certeza sobre el evento o los posibles resultados de una acción. (Volviendo a Lewis[1980], el principio de que, aproximadamente, las probabilidades subjetivas previas condicionadas a las oportunidades objetivas deben ser iguales a las oportunidades objetivas se denomina principio principal). Además, la probabilidad debe considerarse en relación con un período de tiempo fijo y bien definido. Para el concepto de probabilidad que incluye probabilidades objetivas y subjetivas, en general, véase Hájek (2011).
- 22Para los lectores bien versados en teorías económicas de las ciencias de la decisión, debería añadirse que, dependiendo de la teoría particular, las probabilidades no siempre se asignan a las consecuencias de las alternativas de acción (por ejemplo, Jeffrey, 1983), sino también, por ejemplo y más a menudo, a los llamados estados del mundo (por ejemplo, Savage, 1954).
- 23La fórmula de riesgo «Riesgo = probabilidad * medida de severidad (por ejemplo, utilidad, unidad monetaria, etc.)» se deriva directamente del concepto de Riesgo II (cuarta definición de Hansson). Dado que el riesgo II presupone probabilidades conocidas (con 0 < p < 1), se toman decisiones bajo el término «riesgo» y no bajo condiciones de «incertidumbre» (quinta definición de Hansson). Y, finalmente, ver el riesgo como probabilidad (tercera definición) puede considerarse un caso especial de Riesgo II.
- 24Una ilustración similar (pero insuficiente) se encuentra en Heinemann (2014, p. 61).
- 25Véase más arriba: «Por lo tanto, es a su vez importante contar con un concepto de riesgo basado en modelos de probabilidad para poder participar y contribuir al discurso del riesgo si se quiere llegar a un gran número de participantes y economistas o personas interesadas en la gestión del riesgo en la banca, en particular. Sin embargo, dado que tal definición de riesgo (que será bautizada como Riesgo II) no haría justicia a los requisitos establecidos anteriormente (por ejemplo, la primera condición), no será la que se persiga y adopte en este estudio después de todo».
- 26Diferenciamos entre cuatro tipos de escalas: nominal, ordinal, intervalo y proporción. Según Tal (2015, 3.2), «las escalas nominales representan objetos que pertenecen a clases que no tienen un orden particular, por ejemplo, masculino y femenino. Las escalas ordinales representan el orden pero no la estructura algebraica» y admiten cualquier función de transformación mientras sea monótona y en aumento. Celsius es un ejemplo de escalas de intervalos: «representan igualdad o desigualdad entre intervalos de temperatura, pero no relaciones de temperatura, porque sus puntos cero son arbitrarios. La escala Kelvin, por el contrario, es una escala de proporción, al igual que las conocidas escalas que representan la masa en kilogramos, la longitud en metros y la duración en segundos». Esta clasificación se perfeccionó aún más para distinguir entre escalas de intervalos lineales y logarítmicos y entre escalas de relación con y sin unidad natural (Tal, 2015, 3.2.). «Las escalas de razón con una unidad natural, como las utilizadas para contar objetos discretos y para representar probabilidades, se denominaron escalas “absolutas”» (Tal, 2015, 3.2.).
- 27Es una cuestión abierta si la representación de las magnitudes en escalas ordinales debe contar como medida en absoluto (Tal, 2015).


